题目内容
10.设奇函数y=f(x)的定义域为R,且满足f(x-2)=-f(x)对任意x∈R恒成立,当-1≤x≤1时,f(x)=x3.则下列三个命题:①y=f(x)是以4为周期的周期函数;
②y=f(x)在[1,3]上的解析式为f(x)=(2-x)3;
③x=1与x=-1,都是函数y=f(x)图象的对称轴.
其中正确的命题是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
分析 对于①,由f(x-2)=-f(x)对一切x∈R恒成立即可判断①的正误;对于②,利用①f(x)是以4为周期的周期函数,当-1≤x≤1时,f(x)=x3即可求得f(x)在[1,3]上的解析式,从而可判断其正误;对于③,由f(1+x)=f(1-x)与f(-1+x)=f(-1-x)即可判断③的正误;
解答 解:对于①,∵f(x-2)=-f(x)对一切x∈R恒成立,
∴f[(x-2)-2]=-f(x-2)=f(x),即f(x-4)=f(x)
以-x代x得:f(-x-4)=f(-x),
又函数y=f(x)是定义域为R的奇函数,
∴-f(x+4)=-f(x),
∴f(x+4)=f(x),
∴f(x)是以4为周期的周期函数,故①正确;
对于②,令1≤x≤3,则-1≤2-x≤1,故-1≤x-2≤1,
∵-1≤x≤1时,f(x)=x3,
∴f(x-2)=(x-2)3;
∵f(x-2)=-f(x),
∴-f(x)=(x-2)3,
∴f(x)=(2-x)3,故②正确;
∵f(x-2)=-f(x),
∴f[-1+(x-1)]=f[-1-(x-1)]=-f(x),
∴f(x)的图象关于x=-1对称;
∵f(2-x)=f(x),
∴f[1+(1-x)]=f[1-(1-x)],
∴f(x)的图象关于x=1对称,
故③正确.
∴正确的命题是①②③.
故答案为:①②③.
点评 本题考查命题的真假判断与应用,考查函数的周期性及函数解析式的求解及常用方法,综合性强,属于中档题

练习册系列答案
相关题目
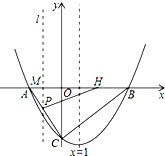 如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.
如图,在平面直角坐标系xOy中,抛物线y=ax2+bx-4与x轴交于点A(-2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.