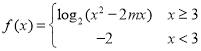题目内容
【题目】已知函数![]() ,
,![]() ,
,![]()
(1)若函数f(x)有两个零点,求实数a的取值范围;
(2)若a=3,且对任意的x1∈[-1,2],总存在![]() ,使g(x1)-f(x2)=0成立,求实数m的取值范围.
,使g(x1)-f(x2)=0成立,求实数m的取值范围.
【答案】(1)![]()
(2)![]()
【解析】
(1)令t=x2,则t∈[1,3],记![]() ,问题转化为函数y=h(t)与y=a有两个交点,利用函数的导数判断函数的单调性求解函数的最小值然后求解实数a的范围.
,问题转化为函数y=h(t)与y=a有两个交点,利用函数的导数判断函数的单调性求解函数的最小值然后求解实数a的范围.
(2)由(1)知f(x)∈[1,2],记A=[1,2],通过当m=0时,当m>0时,当m<0时,分类求实数m的取值范围,推出结果即可.
(1)由题意,函数![]() ,
,![]() ,
,
令t=x2,则t∈[1,3],则![]() ,
,
要使得函数f(x)有两个零点,即函数y=h(t)与y=a有两个交点,
因为![]() ,当t∈(1,2)时,
,当t∈(1,2)时,![]() <0;当t∈(2,3)时,
<0;当t∈(2,3)时,![]() >0,
>0,
所以函数h(t)在(1,2)递减,(2,3)递增,
从而h(t)min=h(2)=4,![]() ,h(1)=5,
,h(1)=5,
由图象可得,当![]() 时,y=h(t)与y=a有两个交点,
时,y=h(t)与y=a有两个交点,
所以函数f(x)有两个零点时实数a的范围为:![]() .
.
(2)由(1)知f(x)∈[1,2],记A=[1,2],
当m=0时,![]() ,显然成立;
,显然成立;
当m>0时,![]() 在[-1,2]上单调递增,所以
在[-1,2]上单调递增,所以![]() ,
,
记![]() ,
,
由对任意的![]() ,总存在
,总存在![]() ,使
,使![]() 成立,可得
成立,可得![]() ,
,
所以![]() 且
且![]() ,解得
,解得![]() ,
,
当m<0时,![]() 在[-1,2]上单调递减,所以
在[-1,2]上单调递减,所以![]() ,
,
所以![]() 且
且![]() ,截得
,截得![]() ,
,
综上,所求实数m的取值范围为![]() .
.

练习册系列答案
相关题目