题目内容
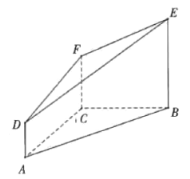
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .三角形
.三角形![]() 的两条边
的两条边![]() ,
,![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() .
.
(1)求点![]() 的轨迹方程;
的轨迹方程;
(2)设直线![]() 方程为
方程为![]() ,直线
,直线![]() 方程为
方程为![]() ,直线
,直线![]() 交
交![]() 于
于![]() ,点
,点![]() ,
,![]() 关于
关于![]() 轴对称,直线
轴对称,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() .若
.若![]() 的面积为
的面积为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)本题可以先将点![]() 的坐标设出,然后写出直线
的坐标设出,然后写出直线![]() 的斜率与直线
的斜率与直线![]() 的斜率,最后根据
的斜率,最后根据![]() 、
、![]() 所在直线的斜率之积是
所在直线的斜率之积是![]() 即可列出算式并通过计算得出结果;
即可列出算式并通过计算得出结果;
(2)首先可以联立直线![]() 的方程与直线
的方程与直线![]() 的方程,得出点
的方程,得出点![]() 两点的坐标,然后联立直线
两点的坐标,然后联立直线![]() 的方程与点
的方程与点![]() 的轨迹方程得出
的轨迹方程得出![]() 点坐标并写出直线
点坐标并写出直线![]() 的方程,最后求出
的方程,最后求出![]() 点坐标并根据三角形面积公式计算出
点坐标并根据三角形面积公式计算出![]() 的值。
的值。
(1)设点![]() 的坐标为
的坐标为![]() ,因为点
,因为点![]() 的坐标分别为
的坐标分别为![]() 、
、![]() ,
,
所以直线![]() 的斜率
的斜率![]() ,直线
,直线![]() 的斜率
的斜率![]() ,
,
由题目可知![]() ,化简得点
,化简得点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)直线![]() 的方程为
的方程为![]() ,与直线
,与直线![]() 的方程
的方程![]() 联立,
联立,
可得点![]() ,故
,故![]() .
.
将![]() 与
与![]() 联立,消去
联立,消去![]() ,整理得
,整理得![]() ,
,
解得![]() ,或
,或![]() ,根据题目可知点
,根据题目可知点![]() ,
,
由![]() 可得直线
可得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,解得
,解得![]() ,故
,故![]() ,
,
所以![]() ,
,![]() 的面积为
的面积为![]()
又因为![]() 的面积为
的面积为![]() ,故
,故![]() ,
,
整理得![]() ,解得
,解得![]() ,所以
,所以![]() 。
。

【题目】为了研究“教学方式”对教学质量的影响,某高中老师分别用两种不同的教学方式对入学数学平均分数和优秀率都相同的甲、乙两个高一新班进行教学(勤奋程度和自觉性都一样).以下茎叶图为甲、乙两班(每班均为20人)学生的数学期末考试成绩.

甲班 | 乙班 | 合计 | |
优秀 | |||
不优秀 | |||
合计 |
![]() 现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
现从甲班数学成绩不低于80分的同学中随机抽取两名同学,求成绩为87分的同学至少有一名被抽中的概率;
(II)学校规定:成绩不低于75分的为优秀.请填写下面的2×2列联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
下面临界值表供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | .024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2=![]() )
)
【题目】现对某市工薪阶层关于“楼市限购令”的态度进行调查,随机抽调了50人,他们月收入的频数分布及对“楼市限购令”赞成人数如下表.
月收入(单位百元) |
|
|
|
|
|
|
频数 | 5 | 10 | 15 | 10 | 5 | 5 |
赞成人数 | 4 | 8 | 12 | 5 | 2 | 1 |
(1)由以上统计数据填下面2×2列联表,并问是否有99%的把握认为“月收入以5500元为分界点对“楼市限购令”的态度有差异;
月收入不低于55百元的人数 | 月收入低于55百元的人数 | 合计 | |
赞成 | a=______________ | c=______________ | ______________ |
不赞成 | b=______________ | d=______________ | ______________ |
合计 | ______________ | ______________ | ______________ |
(2)试求从年收入位于![]() (单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
(单位:百元)的区间段的被调查者中随机抽取2人,恰有1位是赞成者的概率。
参考公式: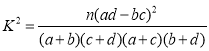 ,其中
,其中![]() .
.
参考值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |