题目内容
【题目】已知函数f(x)是定义在R上的奇函数,且当x≥0时f(x)= ![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)的单调性(不必证明);
(3)若对任意的t∈R,不等式f(k﹣3t2)+f(t2+2t)≤0恒成立,求k的取值范围.
【答案】
(1)
解:∵当x≥0时有 ![]() ,
,
∴当x≤0时,﹣x≥0,
![]()
∴ ![]() (x≤0),
(x≤0),
∴ 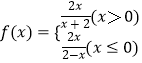
(2)
解:∵当x≥0时有 ![]() ,∴f(x)在[0,+∞)上是增函数
,∴f(x)在[0,+∞)上是增函数
又∵f(x)是奇函数,∴f(x)是在(﹣∞,+∞)上是增函数
(注:只判断f(x)是在(﹣∞,+∞)上是增函数)
(3)
解:f(k﹣3t2)+f(t2+2t)≤0则f(t2+2t)≤﹣f(k﹣3t2)=f(3t2﹣k)
因f(x)为增函数,由上式推得,t2+2t≤3t2﹣k,∴2t2﹣2t﹣k≥0
即对一切t∈R恒有2t2﹣2t﹣k≥0
从而判别式△=4+8k≤0,∴ ![]()
【解析】(1)依题意,当x≤0时,﹣x≥0,利用 ![]() ,可求得当x≤0时的函数表达式,从而可得f(x)的解析式;(2)当x≥0时,将函数
,可求得当x≤0时的函数表达式,从而可得f(x)的解析式;(2)当x≥0时,将函数 ![]() 分离出常数2,利用反比例函数的单调性可判断出f(x)在[0,+∞)上是增函数,再利用奇函数的单调性质,可判断f(x)的单调性;(3)利用(2)可知,f(x)在(﹣∞,+∞)上是增函数,再利用奇函数的性质,将不等式f(k﹣3t2)+f(t2+2t)≤0转化为t2+2t≤3t2﹣k恒成立,利用判别式△=4+8k≤0即可求得k的取值范围.
分离出常数2,利用反比例函数的单调性可判断出f(x)在[0,+∞)上是增函数,再利用奇函数的单调性质,可判断f(x)的单调性;(3)利用(2)可知,f(x)在(﹣∞,+∞)上是增函数,再利用奇函数的性质,将不等式f(k﹣3t2)+f(t2+2t)≤0转化为t2+2t≤3t2﹣k恒成立,利用判别式△=4+8k≤0即可求得k的取值范围.
【考点精析】解答此题的关键在于理解函数的单调性的相关知识,掌握注意:函数的单调性是函数的局部性质;函数的单调性还有单调不增,和单调不减两种.

练习册系列答案
相关题目