题目内容
【题目】已知a1=3，an=2an﹣1+（t+1）2n+3m+t（t，m∈R，n≥2，n∈N*）
（1）t=0，m=0时，求证： 
是等差数列；
（2）t=﹣1，m= 
是等比数列；
（3）t=0，m=1时，求数列{an}的通项公式和前n项和．
【答案】
（1）解：证明：t=0，m=0时，an=2an﹣1+2n，
两边同除以2n，可得 
= 
+1，
即有 
是首项为 
，公差为1的等差数列
（2）解：证明：t=﹣1，m= 
时，an=2an﹣1+3，
两边同加上3，可得an+3=2（an﹣1+3），
即有数列{an+3}为首项为6，公比为2的等比数列
（3）解：t=0，m=1时，an=2an﹣1+2n+3，
两边同除以2n，可得 = +1+ 
，
即为 = =1+ ，
即有得 = 
+（ 
﹣ ）+（ 
﹣ ）+…+（ ﹣ ）
= +1+ 
+1+ 
+…+1+ ，
=n﹣1+ 
=n+2﹣ ，
则an=（n+2）2n﹣3，
前n项和Sn=32+422+523+…+（n+2）2n﹣3n，
可令Rn=32+422+523+…+（n+2）2n，
2Rn=322+423+524+…+（n+2）2n+1，
两式相减可得，﹣Rn=32+22+23+…+2n﹣（n+2）2n+1
=4+ 
﹣（n+2）2n+1
=2﹣（n+1）2n+1，
则Rn═（n+1）2n+1﹣2，
Sn=（n+1）2n+1﹣2﹣3n
【解析】（1）两边同除以2n ， 由等差数列的定义，即可得证；（2）两边同加上3，由等比数列的定义，即可得证；（3）两边同除以2n ， 可得 = +1+ ，即为 = =1+ ，再由数列恒等式，可得数列{an}的通项公式；再由错位相减法和等比数列的求和公式，计算即可得到所求和．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系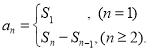
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
