题目内容
【题目】设x，y满足约束条件 
，若目标函数2z=2x+ny（n＞0），z的最大值为2，则y=tan（nx+ 
）的图象向右平移 后的表达式为（ ）
A.y=tan（2x+ ）
B.y=tan（x﹣ ）
C.y=tan（2x﹣ ）
D.y=tan2x
【答案】C
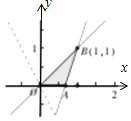
【解析】解：作出x，y满足约束条件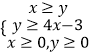 
下的可行域，目标函数2z=2x+ny（n＞0）可化为：y= 
+ 
，基准线y= ， 由线性规划知识，可得当直线z=x+ 
过点B（1，1）时，z取得最大值，即1+ 
=2，解得n=2；
则y=tan（nx+ 
）的图象向右平移 个单位后得到的解析式为y=tan[2（x﹣ ）+ ]=tan（2x﹣ ）．
故选：C．
画出约束条件的可行域，利用z的最大值求出n，利用三角函数的图象变换化简求解即可．
练习册系列答案
名校课堂系列答案
相关题目
