Question

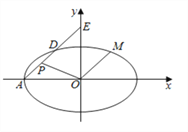
【题目】已知圆点, 是圆上任意一点，线段的垂直平分线和半径相交于点。

（Ⅰ）当点在圆上运动时，求点的轨迹方程；

（Ⅱ）直线与点的轨迹交于不同两点和，且（其中 O 为坐标

原点），求的值.

Answer 1

【答案】（1）（2）

【解析】试题分析：（Ⅰ）化圆的一般方程为标准方程，求出圆心坐标和半径，结合已知可得点Q的轨迹是椭圆，并求出， 的值，进一步得到的值，则椭圆方程可求；（Ⅱ）联立直线方程和椭圆方程，化为关于的一元二次方程，利用韦达定理可得， 的横坐标的和与积，再由，即可求出的值.

试题解析：（I）配方，圆

由条件， ，故点的轨迹是椭圆， ，

椭圆的方程为

（II）将代入得.

由直线与椭圆交于不同的两点，得

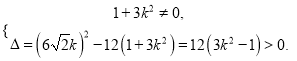即.

设，则.

由,得.

而

.

于是.解得.故的值为.