题目内容
9.在△ABC中,角A,B,C所对的边分别为a,b,c,若bcosA+acosB=$\sqrt{2}$c•cosB,则角B的大小为$\frac{π}{4}$.分析 由条件利用正弦定理、诱导公式、两角和的正弦公式,求得cosB的值,可得B的值.
解答 解:△ABC中,若bcosA+acosB=$\sqrt{2}$c•cosB,则由正弦定理可得 sinBcosA+sinAcosB=$\sqrt{2}$sinC•cosB,
即 sin(A+B)=sinC=$\sqrt{2}$sinC•cosB,求得cosB=$\frac{\sqrt{2}}{2}$,可得B=$\frac{π}{4}$,
故答案为:$\frac{π}{4}$.
点评 本题主要考查正弦定理、诱导公式、两角和的正弦公式,属于基础题.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
19.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$是两个不共线的向量,若$\overrightarrow{AB}$=λ1$\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{AC}$=$\overrightarrow{a}$+λ2$\overrightarrow{b}$(λ1,λ2∈R),则“A,B,C三点共线”是“λ1•λ2-1=0”的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
1.已知集合M={x|1<x<4},N={x|x=2a+1,a∈M},则集合M∪N=( )
| A. | (3,9) | B. | (3,4) | C. | (3,8) | D. | (1,9) |
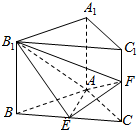 如图,在直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E、F分别为BC、CC1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,E、F分别为BC、CC1的中点.