题目内容
已知函数f(x)=x2-4sinθ•x-1,x∈[-1,
],其中θ∈[0,2π]
(1)当θ=
时,求函数f(x)的最大最小值;
(2)求θ的取值范围,使y=f(x)在区间[-1,
]上存在反函数.
| 3 |
(1)当θ=
| π |
| 6 |
(2)求θ的取值范围,使y=f(x)在区间[-1,
| 3 |
(1)当θ=
时,f(x)=x2-2x-1=(x-1)2-2,
函数的图象为开口向上的抛物线,对称轴为x=1,
故当x∈[-1,1]时,函数单调递减,
当x∈[1,
]时,函数单调递增,
故当x=1时,函数取最小值f(1)=-2,
当x=-1时,函数取最大值f(-1)=2;
(2)可得f(x)=(x-2sinθ)2-1-4sin2θ,
函数的图象为开口向上的抛物线,对称轴为x=2sinθ,
要使函数y=f(x)在区间[-1,
]上存在反函数,
必须使函数在该区间单调,故2sinθ≤-1,或2sinθ≥
,
可得sinθ≤-
,或sinθ≥
,
解之可得
≤θ≤
,或
≤θ≤
,
故θ的取值范围为:
≤θ≤
,或
≤θ≤
| π |
| 6 |
函数的图象为开口向上的抛物线,对称轴为x=1,
故当x∈[-1,1]时,函数单调递减,
当x∈[1,
| 3 |
故当x=1时,函数取最小值f(1)=-2,
当x=-1时,函数取最大值f(-1)=2;
(2)可得f(x)=(x-2sinθ)2-1-4sin2θ,
函数的图象为开口向上的抛物线,对称轴为x=2sinθ,
要使函数y=f(x)在区间[-1,
| 3 |
必须使函数在该区间单调,故2sinθ≤-1,或2sinθ≥
| 3 |
可得sinθ≤-
| 1 |
| 2 |
| ||
| 2 |
解之可得
| 7π |
| 6 |
| 11π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |
故θ的取值范围为:
| 7π |
| 6 |
| 11π |
| 6 |
| π |
| 3 |
| 2π |
| 3 |

练习册系列答案
相关题目




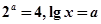 ,则
,则 ;
;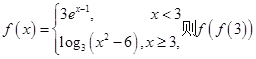 的值为__________.
的值为__________.