题目内容
【题目】某企业常年生产一种出口产品,根据预测可知,进入21世纪以来,该产品的产量平稳增长.记2009年为第1年,且前4年中,第x年与年产量f(x) 万件之间的关系如下表所示:
x | 1 | 2 | 3 | 4 |
f(x) | 4.00 | 5.58 | 7.00 | 8.44 |
若f(x)近似符合以下三种函数模型之一:f(x)=ax+b,f(x)=2x+a,f(x)=log![]() x+a.
x+a.
(1)找出你认为最适合的函数模型,并说明理由,然后选取其中你认为最适合的数据求出相应的解析式;
(2)因遭受某国对该产品进行反倾销的影响,2015年的年产量比预计减少30%,试根据所建立的函数模型,确定2015年的年产量.
【答案】(1) f(x)=![]() x+
x+![]() ,x∈N. (2) 9.1万件.
,x∈N. (2) 9.1万件.
【解析】试题分析:(1)分别代人不同模型,确定a,b值,再代人第三或四个量验证是否符合(2)先按模型计算2015年的年产量,再计算实际年产量.
试题解析:解:(1)符合条件的是f(x)=ax+b.
若模型为f(x)=2x+a,则由f(1)=21+a=4,得a=2,即f(x)=2x+2,
此时f(2)=6, f(3)=10, f(4)=18,与已知相差太大,不符合.
若模型为f(x)=log![]() x+a,则f(x)是减函数,与已知不符合.
x+a,则f(x)是减函数,与已知不符合.
由已知得![]() 解得
解得![]()
所以f(x)=![]() x+
x+![]() ,x∈N.
,x∈N.
(2)2015年预计年产量为f(7)=![]() ×7+
×7+![]() =13,2015年实际年产量为13×(1-30%)=9.1,
=13,2015年实际年产量为13×(1-30%)=9.1,
答:最适合的模型解析式为f(x)=![]() x+
x+![]() ,x∈N .2015年的实际产量为9.1万件.
,x∈N .2015年的实际产量为9.1万件.

【题目】某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合 计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合 计 | 70 | 30 | 100 |
⑴根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差
异”;
⑵已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机
抽取3人,求至多有1人喜欢甜品的概率.
| 0.100 | 0.050 | 0.010 |
| 2.706 | 3.841 | 6.635 |
附: 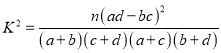 ,
,