题目内容
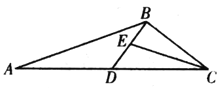
【题目】如图，在凸四边形ABCD中，M为边AB的中点，且MC=MD.分别过点C、D作边BC、AD的垂线，设两条垂线的交点为P.过点P作
与Q.求证：
.
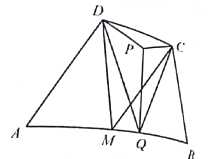
【答案】见解析
【解析】
如图，连结PA、PB，分别取PA、PB的中点E、F，连结EM、ED、FM、FC，则四边形PEMF为平行四边形，从而∠PEM=∠PFM.
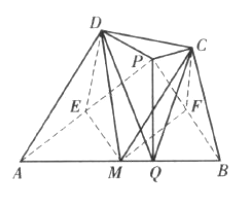
由
，
，MD=MC，
所以
，即∠DEM=∠MFC，所以
∠PED=∠DEM-∠PEM=∠ MFC-∠PFM=∠PFM.
又∠PED=2∠PAD, ∠PFC=2∠PBC,得∠PAD=∠PBC.
由于∠PQA=∠PDA=90°，∠POB=∠PCB=90°，
则P、Q、A、D和P、Q、B、C分别四点共圆.
故∠PQD=∠PAD, ∠PQC=∠PBC,所以∠PQC=∠PQD.
【题目】某地实施乡村振兴战略，对农副产品进行深加工以提高产品附加值，已知某农产品成本为每件3元，加工后的试营销期间，对该产品的价格与销售量统计得到如下数据：
单价x（元） | 6 | 6.2 | 6.4 | 6.6 | 6.8 | 7 |
销量y（万件） | 80 | 74 | 73 | 70 | 65 | 58 |
数据显示单价x与对应的销量y满足线性相关关系．
（1）求销量y（件）关于单价x（元）的线性回归方程
；
（2）根据销量y关于单价x的线性回归方程，要使加工后收益P最大，应将单价定为多少元？（产品收益=销售收入-成本）．
参考公式：
=
=
，
【题目】随着“互联网+交通”模式的迅猛发展，“共享自行车”在很多城市相继出现。某运营公司为了了解某地区用户对其所提供的服务的满意度，随机调查了40个用户，得到用户的满意度评分如下：
用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | 用户编号 | 评分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系统抽样法从40名用户中抽取容量为10的样本，且在第一分段里随机抽到的评分数据为92.
（1）请你列出抽到的10个样本的评分数据；
（2）计算所抽到的10个样本的均值
和方差
；
（3）在（2）条件下，若用户的满意度评分在
之间，则满意度等级为“
级”。试应用样本估计总体的思想，根据所抽到的10个样本，估计该地区满意度等级为“级”的用户所占的百分比是多少？
（参考数据：
）
