Question

【题目】记

（I）若对任意的x0恒成立，求实数a的值；

（II）若直线l:与的图像相切于点Q(m，n) ；

（i）试用m表示a与k；

（ii）若对给定的k，总存在三个不同的实数a1，a2，a3，使得直线l与曲线，，同时相切，求实数k的取值范围。

Answer 1

【答案】（I）（II）（i）.（ii）见解析

【解析】

（I）利用说明是的最大值，也是极大值，求得a，再证明必要性；

（II）（i）利用导数的几何意义及切点既在曲线上又在直线上，列出方程组，解得a，k.

（ii）根据题意求得方程：有三个不同的解时的k的范围，再去证明与a是一一对应的.

（I）∵

∵，又∵恒成立，∴是的最大值

∴，∴；

反过来，当时，单调递减，又，∴在（0，1）上递增，在（1，上递减，，∴恒成立.

∴

（II）（i）∵，由切点，则有：

，

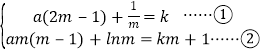把①代入②可得：，

代入①式得：（**），

（ii）根据题意方程（**）有三个不同的解，

令

∴

=

=

由，解得两根分别为与

∴当时，，单调递减；

当时，，单调递增；

当时，，单调递减

∴的极小值为；的极大值为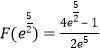

又∵时，

∴当时，方程（**）有三个不同的根，

下面说明三个不同的对应的也是不同的：

设方程（**）的三个不同的根分别为：，且

则有：，，，显然

只需说明即可，

又由可得：

即，假设，

则有，即

即

即，令，即

设

∴

∴在上是减函数，即，与矛盾

∴假设不真，即

∴当，存在三个不同的实数使得直线与曲线，，同时相切．