题目内容
定义在R上的函数f(x)满足f(m+n2)=f(m)+2[f(n)]2,m,n∈R,且f(1)≠0,则f(2 014)=________.
1 007
令m=n=0,得f(0+02)=f(0)+2[f(0)]2,所以f(0)=0;令m=0,n=1,
得f(0+12)=f(0)+2[f(1)]2,
由于f(1)≠0,所以f(1)=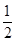 ;令m=x,n=1,得f(x+12)=f(x)+2[f(1)]2,
;令m=x,n=1,得f(x+12)=f(x)+2[f(1)]2,
所以f(x+1)=f(x)+2×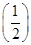 2,
2,
即f(x+1)=f(x)+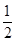 ,
,
这说明数列{f(x)}(x∈Z)是首项为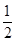 ,公差为
,公差为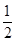 的等差数列,所以f(2 014)=
的等差数列,所以f(2 014)=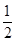 +(2 014-1)×
+(2 014-1)×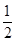 =1 007.
=1 007.
得f(0+12)=f(0)+2[f(1)]2,
由于f(1)≠0,所以f(1)=
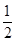 ;令m=x,n=1,得f(x+12)=f(x)+2[f(1)]2,
;令m=x,n=1,得f(x+12)=f(x)+2[f(1)]2,所以f(x+1)=f(x)+2×
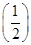 2,
2,即f(x+1)=f(x)+
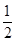 ,
,这说明数列{f(x)}(x∈Z)是首项为
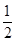 ,公差为
,公差为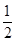 的等差数列,所以f(2 014)=
的等差数列,所以f(2 014)=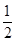 +(2 014-1)×
+(2 014-1)×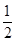 =1 007.
=1 007.
练习册系列答案
 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案 激活思维优加课堂系列答案
激活思维优加课堂系列答案
相关题目
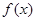 是定义在
是定义在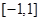 上的奇函数,且
上的奇函数,且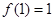 ,若
,若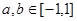 ,
,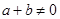 有
有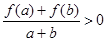 恒成立.
恒成立.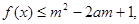 对所有
对所有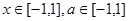 恒成立,求实数
恒成立,求实数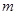 的取值范围.
的取值范围. 与g(x)=
与g(x)= ,表示同一个函数.
,表示同一个函数.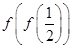 =0.
=0.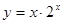 的部分图象如下,其中正确的是( )
的部分图象如下,其中正确的是( )



 ,若f(a)=3,则实数a= _________ .
,若f(a)=3,则实数a= _________ .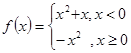 若
若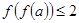 ,则实数
,则实数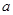 的取值范围是______
的取值范围是______ 则f(2 016)=( )
则f(2 016)=( )
