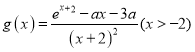题目内容
【题目】已知函数f(x)=﹣alnx+![]() +x(a≠0)
+x(a≠0)
(I)若曲线y=f(x)在点(1,f(1)))处的切线与直线x﹣2y=0垂直,求实数a的值;
(Ⅱ)讨论函数f(x)的单调性;
(Ⅲ)当a∈(﹣∞,0)时,记函数f(x)的最小值为g(a),求证:g(a)≤﹣e﹣4 .
【答案】解:(I)由已知可知f(x)的定义域为{x|x>0}![]() (x>0)
(x>0)
根据题意可得,f′(1)=2×(﹣1)=﹣2
∴﹣a﹣2a2+1=﹣2
∴a=1或a=﹣![]()
(II)∵![]() =
=![]()
①a>0时,由f′(x)>0可得x>2a
由f′(x)<0可得0<x<2a
∴f(x)在(2a,+∞)上单调递增,在(0,2a)上单调递减
②当a<0时,
由f′(x)>0可得x>﹣a
由f′(x)<0可得0<x<﹣a
∴f(x)在(﹣a,+∞)上单调递增,在(0,﹣a)上单调递减
(III)由(II)可知,当a∈(﹣∞,0)时,函数f(x)的最小值f(﹣a)
故g(a)=f(﹣a)=﹣aln(﹣a)﹣3a
则g′(a)=﹣ln(﹣a)﹣4
令g′(a)=0可得﹣ln(﹣a)﹣4=0
∴a=﹣e﹣4
当a变化时,g’(a),g(a)的变化情况如下表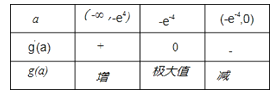
∴a=﹣e﹣4是g(a)在(﹣∞,0)上的唯一的极大值,从而是g(a)的最大值点
当a<0时,![]() =﹣e﹣4
=﹣e﹣4
∴a<0时,g(a)≤﹣e﹣4 .
【解析】(I)先求f(x)的定义域为{x|x>0},先对已知函数进行求导,由f′(1)=﹣2可求a
(II)由![]() =
=![]() 通过比较﹣a与2a的大小解不等式f′(x)>0,f′(x)<0,从而可求函数的单调区间
通过比较﹣a与2a的大小解不等式f′(x)>0,f′(x)<0,从而可求函数的单调区间
(III)由(II)可知,当a∈(﹣∞,0)时,函数f(x)的最小值f(﹣a),结合已知可求a,然后结合已知单调性可求![]() , 从而可证
, 从而可证
【考点精析】认真审题,首先需要了解利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减).
在这个区间单调递减).

 科学实验活动册系列答案
科学实验活动册系列答案