题目内容
2.已知正边形ABCD边长为2,在正边形ABCD内随机取一点P,则点P满足|PA|≤1的概率是$\frac{π}{16}$.分析 由扇形面积公式,结合题意算出满足条件的点P对应的图形的面积,求出正方体ABCD的面积并利用几何概型计算公式,即可算出所求概率.
解答 解:当点P满足|PA|≤1时,P在以A为圆心、半径为1的圆内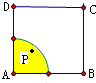
其面积为S′=$\frac{1}{4}$π×12=$\frac{π}{4}$
∵正方形ABCD边长为2,得正方形的面积为S=22=4
∴所求概率为P=$\frac{S′}{S}$=$\frac{\frac{π}{4}}{4}$=$\frac{π}{16}$
故答案为:$\frac{π}{16}$.
点评 本题在正方形中求点P满足条件的概率,着重考查了扇形面积、正方形面积计算公式和几何概型计算公式等知识,属于基础题.

练习册系列答案
相关题目
7.计算lg$\root{5}{1000}$-8${\;}^{\frac{2}{3}}$$-{10^{-lg\frac{5}{3}}}$的值为 ( )
| A. | -$\frac{17}{5}$ | B. | $-\frac{26}{15}$ | C. | $-\frac{76}{15}$ | D. | -4 |
11.已知等差数列{an}中,a5=8,a2=17,则公差d=( )
| A. | -3 | B. | 3 | C. | -9 | D. | 9 |
12.从高处海平面h米的小岛看到正东方向有一只船俯角为30°,南偏西60°方向有一只船俯角为45°,则此时两船间的距离为( )
| A. | 2h米 | B. | $\sqrt{3}$h米 | C. | $\sqrt{7}$h米 | D. | 7h米 |