题目内容
7.已知△ABC中,A=$\frac{π}{3}$,B=$\frac{π}{4}$,a=3,则b=( )| A. | $\frac{3\sqrt{6}}{2}$ | B. | $\sqrt{6}$ | C. | 3$\sqrt{2}$ | D. | $\frac{3\sqrt{2}}{2}$ |
分析 由正弦定理列出关系式,把sinA,sinB以及a的值,求出b的值.
解答 解:∵在△ABC中,A=$\frac{π}{3}$,B=$\frac{π}{4}$,a=3,
∴由正弦定理$\frac{a}{sinA}$=$\frac{b}{sinB}$得:b=$\frac{asinB}{sinA}$=$\frac{3×\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}}$=$\sqrt{6}$,
故选:B.
点评 此题考查了正弦定理,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.集合M={x|-1<x<1},N={x|0<x<2},则M∩N=( )
| A. | {x|-1<x<1} | B. | {x|0<x<2} | C. | {x|0<x<1} | D. | {x|-1<x<2} |
12.已知函数f(x)=x2-4ax+2a+6(a∈R)
(1)若函数f(x)在区间[-2,3]上是单调函数,求a的取值范围;
(2)若函数f(x)的值域为非负数,求函数g(a)=2-a|a+3|的最值.
(1)若函数f(x)在区间[-2,3]上是单调函数,求a的取值范围;
(2)若函数f(x)的值域为非负数,求函数g(a)=2-a|a+3|的最值.
19.设函数f(x)=x2+(a-2)x-1在区间[2,+∞)上是增函数,则实数a的最小值为( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
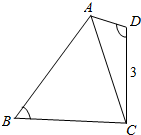 如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=$\frac{\sqrt{3}}{3}$
如图所示,在四边形ABCD中,∠D=2∠B,且AD=1,CD=3,cos∠B=$\frac{\sqrt{3}}{3}$