Question

【题目】某厂生产的产品在出厂前都要做质量检测，每件一等品都能通过检测，每件二等品通过检测的概率为．现有件产品，其中件是一等品， 件是二等品．

（Ⅰ）随机选取件产品，设至少有一件通过检测为事件，求事件的概率；

（Ⅱ）随机选取件产品，其中一等品的件数记为，求的分布列及数学期望.

Answer 1

【答案】(Ⅰ) ; （Ⅱ）见解析.

【解析】试题分析：

（Ⅰ）“至少有一件通过检测”的反面是“没有一件通过检测”，即三件都不通过，利用互斥事件的概率可得；

（Ⅱ）求的分布列，首先要确定变量的取值，由于10件中有6件一等品，因此的取值依次为，由古典概型概率公式可得各概率，从而得分布列，再由期望公式可计算出期望．

试题解析：

(Ⅰ)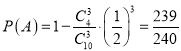

所以随机选取3件产品，至少有一件通过检测的概率为.

（Ⅱ）由题可知可能取值为.

, ,

, .

则随机变量的分布列为

	0	1	2	3