题目内容
【题目】已知α∈(0, ![]() ),β∈(0,π),且tan(α﹣β)=
),β∈(0,π),且tan(α﹣β)= ![]() ,tanβ=﹣
,tanβ=﹣ ![]() .
.
(1)求tanα;
(2)求2α﹣β的值.
【答案】
(1)解:∵2α﹣β=2(α﹣β)+β,
又tan(α﹣β)= ![]() ,
,
∴tan2(α﹣β)= ![]() =
= ![]() .
.
故tan(2α﹣β)=tan[2(α﹣β)+β]= ![]() =
= 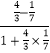 =1.
=1.
∴tanα=tan[(α﹣β)+β]= ![]() =
= ![]() .
.
(2)解:∵0<α< ![]() ,
,
∴0<2α< ![]() .
.
又∵tanβ=﹣ ![]() ,且β∈(0,π)β∈(
,且β∈(0,π)β∈( ![]() ,π)﹣β∈(﹣π,﹣
,π)﹣β∈(﹣π,﹣ ![]() ).
).
∴2α﹣β∈(﹣π,0).又由(1)可得tan(2α﹣β)=1,
∴2α﹣β=﹣ ![]() .
.
【解析】(1)观察角度的关系发现2α﹣β=2(α﹣β)+β,求出tan2(α﹣β),然后利用两角和的正切函数求出tan(2α﹣β),进而可求tanα的值.(2)再根据tanα、tanβ的值确定α,β的具体范围,进而确定2α﹣β的范围,就可以根据特殊角的三角函数值求出结果.
【考点精析】解答此题的关键在于理解两角和与差的正切公式的相关知识,掌握两角和与差的正切公式:![]() .
.

练习册系列答案
相关题目