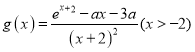题目内容
【题目】已知椭圆![]() 的中心在原点,离心率等于
的中心在原点,离心率等于![]() ,它的一个短轴端点恰好是抛物线
,它的一个短轴端点恰好是抛物线![]() 的焦点
的焦点
(1)求椭圆![]() 的方程;
的方程;
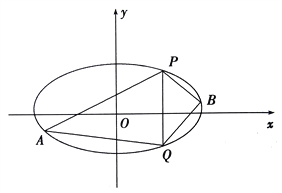
(2)已知![]() 、
、![]() 是椭圆上的两点,
是椭圆上的两点, ![]() ,
, ![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.①若直线
两侧的动点.①若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
②当![]() ,
, ![]() 运动时,满足
运动时,满足![]() ,试问直线
,试问直线![]() 的斜率是否为定值,请说明理由
的斜率是否为定值,请说明理由
【答案】(1)![]() (2)
(2)![]()
【解析】试题分析: (1)由椭圆的离心率及短轴端点坐标求出![]() ,得到椭圆方程; (2)①设
,得到椭圆方程; (2)①设![]() 设直线AB方程为
设直线AB方程为![]() ,联立直线与椭圆方程,消去
,联立直线与椭圆方程,消去![]() ,得到一个关于
,得到一个关于![]() 的二次方程,求出
的二次方程,求出![]() ,再求出
,再求出![]() ,代入三角形面积公式,求出最大值; ②由
,代入三角形面积公式,求出最大值; ②由![]() 得到直线
得到直线![]() 斜率之和为0,设直线
斜率之和为0,设直线![]() 斜率为
斜率为![]() ,则直线
,则直线![]() 斜率为
斜率为![]() ,直线
,直线![]() 方程为
方程为![]() ,代入椭圆方程中,求出
,代入椭圆方程中,求出![]() 的表达式,同理求出
的表达式,同理求出![]() 的表达式,再求出
的表达式,再求出![]() 的值,代入直线
的值,代入直线![]() 的斜率计算公式中,结果为定值.
的斜率计算公式中,结果为定值.
试题解析:(1)![]() ∴
∴![]()
∴![]()
![]() 又
又 ![]()
∴![]()
![]() ∴ 椭圆方程为
∴ 椭圆方程为![]()
(2)①设 ![]() ,
, ![]()
设![]() 方程
方程 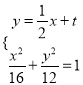 代入化简
代入化简 ![]()
![]() ,
, ![]()
![]() 又
又![]() 、
、![]()
![]()
当![]() 时,
时, ![]() 最大为
最大为![]()
②当![]() 时,
时, ![]() 、
、![]() 斜率之和为
斜率之和为![]() .
.
设![]() 斜率为
斜率为![]() ,则
,则![]() 斜率为
斜率为![]()
设 代入化简 同理 ∴ 直线 点睛:本题主要考查了椭圆的标准方程及性质,直线与椭圆相交问题,一元二次方程根与系数关系,斜率的计算公式,考查了推理与计算能力, 属于难题.![]() 方程
方程![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() 的斜率为定值
的斜率为定值![]()

练习册系列答案
相关题目