题目内容
12.若函数f(x)=ax2+bx+c的图象开口向上且顶点在第四象限,则函数f′(x)的图象是( )| A. | 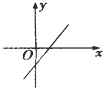 | B. | 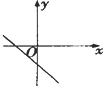 | C. | 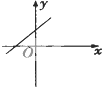 | D. | 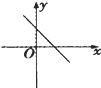 |
分析 先根据二次函数的判断出a,b的符号,再求导,根据一次函数的性质判断所经过的象限即可.
解答 解:∵函数f(x)=ax2+bx+c的图象开口向上且顶点在第四象限,
∴a>0,-$\frac{b}{2a}$>0,
∴b<0,
∵f′(x)=2ax+b,
∴函数f′(x)的图象经过一,三,四象限,
∴选项A符合,
故选:A.
点评 本题考查了导数的运算和一次函数,二次函数的图象和性质,属于基础题.

练习册系列答案
相关题目
3.已知全集U={1,2,3,4,5,6,7,8},集合A={1,4,7},集合B={1,3,4,6,8},则(∁UA)∩B=( )
| A. | {1,4} | B. | {3,6,8} | C. | {1,2,4,5,7} | D. | {2,3,5,6,7,8} |
7.给定81个数排成如图所示的数表,若每行9个数与每列的9个数按表中顺序构成等差数列,且表中正中间一个数a55=5,则表中所有数之和为405.
| a11 | a12 | … | a19 |
| a21 | a22 | … | a29 |
| … | … | … | … |
| a91 | a92 | … | a99 |
1.函数$y=sin(2x+\frac{5π}{2})$的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
2.一个用流程图表示的算法如图所示,则其运行后输出的结果为( )
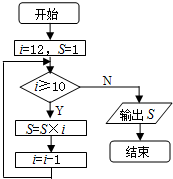

| A. | 1320 | B. | 11880 | C. | 132 | D. | 以上都不对 |
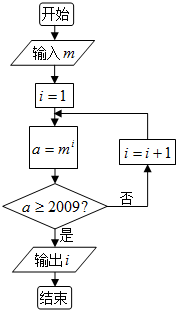 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)