题目内容
在等差数列{an}中,公差为d,前n项和为Sn.在等比数列{bn}中,公比为q,前n项和为S'n(n∈N*).(1)在等差数列{an}中,已知S10=30,S20=100,求S30.
(2)在等差数列{an}中,根据要求完成下列表格,并对①、②式加以证明(其中m、m1、m2、n∈N*).
| 用Sm表示S2m | S2m=2Sm+m2d |
用 、 、 表示 表示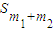 |  =______① =______① |
| 用Sm表示Snm | Snm=______② |
(ⅰ) 类比(2)中①式,在等比数列{bn}中,写出相应的结论.
(ⅱ) (解答本题,最多得5分)类比(2)中②式,在等比数列{bn}中,写出相应的结论.
(ⅲ) (解答本题,最多得6分)在等差数列{an}中,将(2)中的①推广到一般情况.
(ⅳ) (解答本题,最多得6分)在等比数列{bn}中,将(2)中的①推广到一般情况.
【答案】分析:(1)由S10=30,S20=100,得10a1+45d=30,20a1+190d=100,解得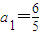 ,
,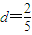 ,由此能求出S30.
,由此能求出S30.
(2)①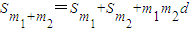 .证明:由
.证明:由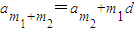 ,知
,知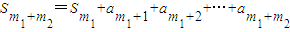 =
=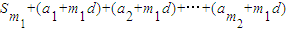 ,由此得证.
,由此得证.
②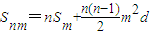 (或写成Snm=nSm+Cn2m2d,n≥2).证明:
(或写成Snm=nSm+Cn2m2d,n≥2).证明: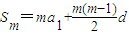 ,
,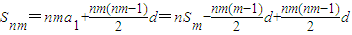 ,由此得证.
,由此得证.
(3)(ⅰ)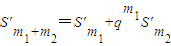 .
.
(ⅱ)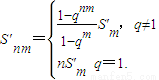 .
.
(ⅲ)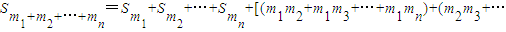 +m2mn)+…+mn-1mn]d,(n≥2).(或写成
+m2mn)+…+mn-1mn]d,(n≥2).(或写成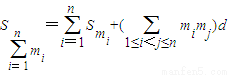 ,(n≥2)).
,(n≥2)).
(ⅳ)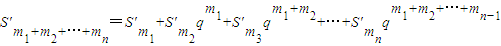 ,(n≥2).
,(n≥2).
解答:解:(1)由S10=30,S20=100,得10a1+45d=30,20a1+190d=100,
解得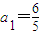 ,
,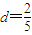 ,…(2分)
,…(2分)
故S30=210. …(4分)
(2)①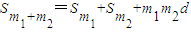 . …(6分)
. …(6分)
证明:∵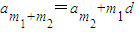 ,
,
∴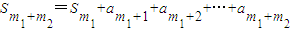
=
=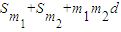 . …(8分)
. …(8分)
②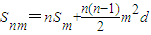 (或写成Snm=nSm+Cn2m2d,n≥2). …(10分)
(或写成Snm=nSm+Cn2m2d,n≥2). …(10分)
证明:∵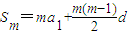 ,
,
∴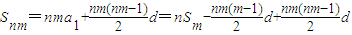
=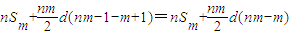
=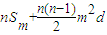 . …(12分)
. …(12分)
(3)(ⅰ)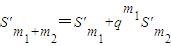 . …(16分)
. …(16分)
(ⅱ)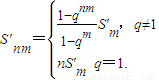 …(17分)
…(17分)
(ⅲ)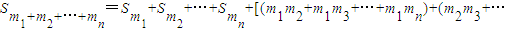 +m2mn)+…+mn-1mn]d,(n≥2).(或写成
+m2mn)+…+mn-1mn]d,(n≥2).(或写成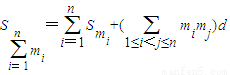 ,(n≥2)). …(18分)
,(n≥2)). …(18分)
(ⅳ)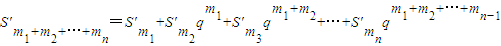 ,(n≥2). …(18分)
,(n≥2). …(18分)
点评:本题考查等差数列和等比数列的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
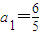 ,
,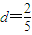 ,由此能求出S30.
,由此能求出S30.(2)①
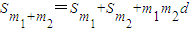 .证明:由
.证明:由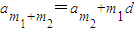 ,知
,知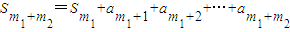 =
=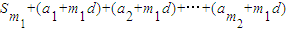 ,由此得证.
,由此得证.②
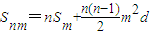 (或写成Snm=nSm+Cn2m2d,n≥2).证明:
(或写成Snm=nSm+Cn2m2d,n≥2).证明: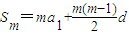 ,
,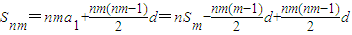 ,由此得证.
,由此得证.(3)(ⅰ)
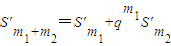 .
.(ⅱ)
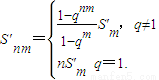 .
.(ⅲ)
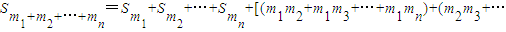 +m2mn)+…+mn-1mn]d,(n≥2).(或写成
+m2mn)+…+mn-1mn]d,(n≥2).(或写成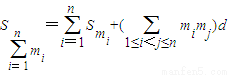 ,(n≥2)).
,(n≥2)).(ⅳ)
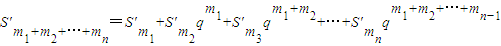 ,(n≥2).
,(n≥2).解答:解:(1)由S10=30,S20=100,得10a1+45d=30,20a1+190d=100,
解得
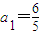 ,
,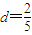 ,…(2分)
,…(2分)故S30=210. …(4分)
(2)①
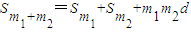 . …(6分)
. …(6分)证明:∵
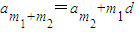 ,
,∴
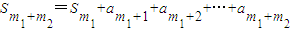
=

=
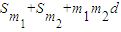 . …(8分)
. …(8分)②
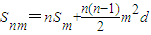 (或写成Snm=nSm+Cn2m2d,n≥2). …(10分)
(或写成Snm=nSm+Cn2m2d,n≥2). …(10分)证明:∵
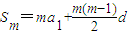 ,
,∴
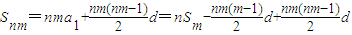
=
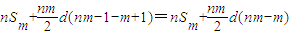
=
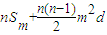 . …(12分)
. …(12分)(3)(ⅰ)
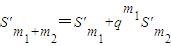 . …(16分)
. …(16分)(ⅱ)
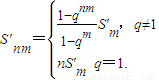 …(17分)
…(17分)(ⅲ)
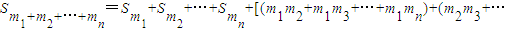 +m2mn)+…+mn-1mn]d,(n≥2).(或写成
+m2mn)+…+mn-1mn]d,(n≥2).(或写成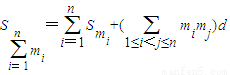 ,(n≥2)). …(18分)
,(n≥2)). …(18分)(ⅳ)
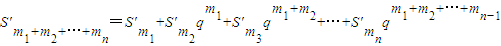 ,(n≥2). …(18分)
,(n≥2). …(18分)点评:本题考查等差数列和等比数列的综合应用,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目