题目内容
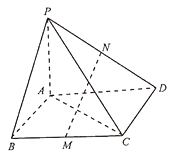
【题目】在四棱锥
中，已知
分别是
的中点，若
是平行四边形，
(1)求证：
平面
(2)若
平面，求证：
【答案】(1)见解析(2)见解析
【解析】
(1) 取PA中点E，根据平几知识可得四边形BMNE为平行四边形，再根据线面平行判定定理得结论，(2)先根据线面垂直判定定理得AC⊥平面PAB，即得AC⊥BE，再根据平行关系得结果.
（1）取PA中点E，连结BE，NE
因为N为PD中点，所以，EN∥AD，且EN＝
AD，
又M为BC中点，
是平行四边形，所以 BM∥AD，且BM＝AD，
所以，BM∥EN且BM＝EN
所以，四边形BMNE为平行四边形，
所以，MN∥BE，而MN
平面PAB，BE
平面PAB
所以，MN∥平面PAB。
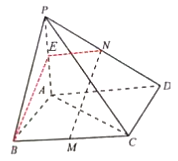
（2）∵
∴AC⊥AB，
∵PA⊥平面ABCD，∴PA⊥AC
∵PA∩AB＝A，∴AC⊥平面PAB，
∵BE平面PAB，∴AC⊥BE
由（1）知，BE∥MN，∴AC⊥MN
练习册系列答案
相关题目
