题目内容
【题目】如图，公路
围成的是一块顶角为
的角形耕地，其中
，在该块土地中
处有一小型建筑，经测量，它到公路的距离分别为
，现要过点修建一条直线公路
，将三条公路围成的区域
建成一个工业园.
（1）以
为坐标原点建立适当的平面直角坐标系，并求出点的坐标；
（2）三条公路围成的工业园区的面积恰为
，求公路所在直线方程.
【答案】(1) 
；(2) 
.
【解析】
(1)以
为坐标原点, 
所在直线为
轴，过点且垂直于的直线为
轴，建立平面直角坐标系.根据条件求出直线
的方程，设出点
坐标，代点到直线的距离公式即可求出所求；
(2)由(1)及题意设出直线
的方程后，即可求得点
的横坐标，与点
的纵坐标，由
求得
后，即可求解.
(1)以为坐标原点, 所在直线为轴，过点且垂直于的直线为轴，
建立如图所示的平面直角坐标系
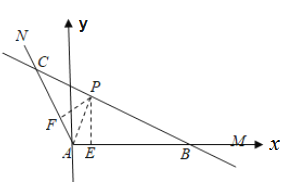
由题意可设点
，且直线的斜率为
，并经过点
，
故直线的方程为：
，
又因点到的距离为
，所以
，解得
或
(舍去)
所以点坐标为.
(2)由题意可知直线的斜率一定存在，故设其直线方程为：
，
与直线的方程：，联立后解得:
，
对直线方程：，令
，得
，
所以
，解得
，
所以直线方程为：
，即:.
练习册系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
