题目内容
若平面α,β的法向量分别为
=(-1,2,4),
=(x,-1,-2),并且α∥β,则x的值为( )
| a |
| b |
| A、10 | ||
| B、-10 | ||
C、
| ||
D、-
|
考点:平面的法向量
专题:空间向量及应用
分析:由题意可得
∥
,可得x的方程,解方程可得.
| a |
| b |
解答:解:∵α,β的法向量分别为
=(-1,2,4),
=(x,-1,-2),并且α∥β,
∴
∥
,∴存在实数λ使
=λ
成立,
∴(-1,2,4)=λ(x,-1,-2),解得x=
故选:C
| a |
| b |
∴
| a |
| b |
| a |
| b |
∴(-1,2,4)=λ(x,-1,-2),解得x=
| 1 |
| 2 |
故选:C
点评:本题考查空间向量的平行和平面的法向量,属基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知直线y=k(x+1)与抛物线C:y2=4x相交于点A,B两点,F为抛物线C的焦点,若|FA|=3|FB|,则k=( )
A、±
| ||||
B、±
| ||||
C、±
| ||||
D、±
|
设f为实系数三次多项式函数.已知五个方程式的相异实根个数如下表所述﹕
关于f的极小值α﹐试问下列选项是正确的﹖( )
| f(x)-20=0 | 1 | f(x)+10=0 | 1 |
| f(x)-10=0 | 3 | f(x)+20=0 | 1 |
| f(x)=0 | 3 |
| A、0<α<10 |
| B、-20<α<-10 |
| C、-10<α<0 |
| D、α不存在 |
复数
(i为虚数单位)在复平面上对应的点在( )
| 2+i |
| i3 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
选择结构不同于顺序结构的明显特征是含有( )
| A、处理框 | B、判断框 | C、起止框 | D、输入、输出框 |
设a=
(1-2x)dx,则二项式(x2+
)6的常数项是( )
| ∫ | 2 0 |
| a |
| x |
| A、-240 | B、240 |
| C、-160 | D、160 |
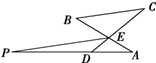 如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.
如图,AB与CD相交于点E,过E作BC的平行线与AD的延长线交于点P,已知∠A=∠C,PD=2DA=2,求PE的长.