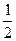题目内容
数列{an}中,a1=-
,其前n项和Sn满足Sn=-
(n≥2),
(1)计算S1,S2,S3,S4;
(2)猜想Sn的表达式并用数学归纳法证明.
| 2 |
| 3 |
| 1 |
| Sn-1+2 |
(1)计算S1,S2,S3,S4;
(2)猜想Sn的表达式并用数学归纳法证明.
(1)∵a1=-
,其前n项和Sn满足Sn=-
(n≥2),
∴S2=-
=-
,S3=-
=-
,S4=-
=-
;
(2)猜想Sn=-
.下面用数学归纳法证明.
①n=1时,结论成立;
②假设n=k时,成立,即可Sk=-
,
则n=k+1时,Sk+1=-
=-
=-
,
即n=k+1时,猜想成立,
①②可知Sn=-
.
| 2 |
| 3 |
| 1 |
| Sn-1+2 |
∴S2=-
| 1 |
| S1+2 |
| 3 |
| 4 |
| 1 |
| S2+2 |
| 4 |
| 5 |
| 1 |
| S3+2 |
| 5 |
| 6 |
(2)猜想Sn=-
| n+1 |
| n+2 |
①n=1时,结论成立;
②假设n=k时,成立,即可Sk=-
| k+1 |
| k+2 |
则n=k+1时,Sk+1=-
| 1 |
| Sk+2 |
| 1 | ||
-
|
| k+2 |
| k+3 |
即n=k+1时,猜想成立,
①②可知Sn=-
| n+1 |
| n+2 |

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案
相关题目
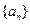 中各项为:
中各项为: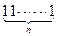
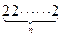 ……,证明这个数列中的每一项都是两个相邻整数的积.
……,证明这个数列中的每一项都是两个相邻整数的积.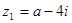 ,
,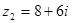 ,
,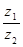 为纯虚数.
为纯虚数.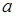 的值;(2)求复数
的值;(2)求复数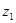 的平方根.
的平方根.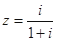 的共轭复数是( )
的共轭复数是( )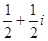



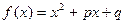
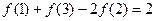
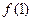 |、|
|、|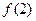 |、|
|、|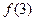 |中至少有一个不小于
|中至少有一个不小于