题目内容
利用数学归纳法证明不等式1+
+
+…
<f(n)(n≥2,n∈N*)的过程中,由n=k变到n=k+1时,左边增加了( )
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
| A.1项 | B.k项 | C.2k-1项 | D.2k项 |
用数学归纳法证明等式1+
+
+…+
<f(n)(n≥2,n∈N*)的过程中,
假设n=k时不等式成立,左边=1+
+
+…+
,
则当n=k+1时,左边=1+
+
+…+
+
+
+…+
,
∴由n=k递推到n=k+1时不等式左边增加了:
+
+…+
,
共(2k+1-1)-2k+1=2k项,
故选:D.
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2n-1 |
假设n=k时不等式成立,左边=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
则当n=k+1时,左边=1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2k-1 |
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+1-1 |
∴由n=k递推到n=k+1时不等式左边增加了:
| 1 |
| 2k |
| 1 |
| 2k+1 |
| 1 |
| 2k+1-1 |
共(2k+1-1)-2k+1=2k项,
故选:D.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
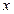
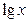


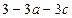


 =
= 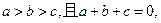 求证
求证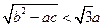 ”索的因应是( )
”索的因应是( )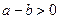 B
B 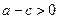 C
C 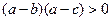 D
D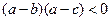
 是虚数单位,复数
是虚数单位,复数 ,则
,则 =( )
=( )