题目内容
【题目】如图是一个“蝴蝶形图案(阴影区域)”,其中![]() 是过抛物线
是过抛物线![]() 的两条互相垂直的弦(点
的两条互相垂直的弦(点![]() 在第二象限),且
在第二象限),且![]() 交于点
交于点![]() ,点
,点![]() 为
为![]() 轴上一点,
轴上一点,![]() ,其中
,其中![]() 为锐角
为锐角

(1)设线段![]() 的长为
的长为![]() ,将
,将![]() 表示为关于
表示为关于![]() 的函数
的函数
(2)求“蝴蝶形图案”面积的最小值,并指出取最小值时![]() 的大小
的大小
【答案】(1)![]() (2)“蝴蝶形图案”面积的最小值为
(2)“蝴蝶形图案”面积的最小值为![]() ,取最小值时
,取最小值时![]() .
.
【解析】
(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]() ,在
,在![]() 中利用三角函数的定义可得
中利用三角函数的定义可得![]() ,
,![]() ,即点
,即点![]() 的坐标为
的坐标为![]() ,代入抛物线的方程,可得
,代入抛物线的方程,可得![]() 关于
关于![]() 的函数.
的函数.
(2)由题意结合图形,![]() 可由
可由![]() 逆时针旋转得到,即可得到
逆时针旋转得到,即可得到![]() 关于
关于![]() 的函数,进而可得“蝴蝶形图案”面积
的函数,进而可得“蝴蝶形图案”面积![]() 关于
关于![]() 的函数,换元后利用配方法求其面积的最小值.
的函数,换元后利用配方法求其面积的最小值.
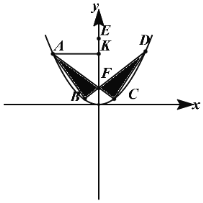
(1)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,![]()
![]() 在
在![]() 中,
中,![]()
![]()
![]()
即:![]() ,
, ![]()
由此可得点![]() 的坐标为
的坐标为![]()
![]() 点
点![]() 是抛物线
是抛物线![]() 上的点,将其代入可得:
上的点,将其代入可得:
![]() ,即:
,即:![]()
解得: ![]()
![]()
![]() 故:
故: ![]()
![]()
![]() 表示为关于
表示为关于![]() 的函数为:
的函数为:![]()
(2)根据(1)得: ![]() 表示为关于
表示为关于![]() 的函数为:
的函数为:![]()
由题意可知: ![]()
![]()
![]() 可由
可由![]() 逆时针旋转
逆时针旋转![]() 得到,其与
得到,其与![]() 正半轴夹角为
正半轴夹角为![]() .
.
![]()
![]()
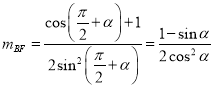
![]()
![]() 可由
可由![]() 逆时针旋转
逆时针旋转![]() 得到,其与
得到,其与![]() 正半轴夹角为
正半轴夹角为![]() .
.
![]()
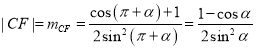
![]()
![]() 可由
可由![]() 逆时针旋转
逆时针旋转![]() 得到,其与
得到,其与![]() 正半轴夹角为
正半轴夹角为![]() .
.
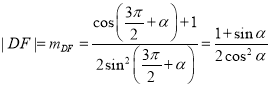
![]()
![]() ,
,![]() ,
,![]()
设“蝴蝶形图案”面积为![]() :
:
![]()
![]()
![]()
![]()
令:![]()
![]()
![]() 为锐角
为锐角
![]()
![]() 则
则![]() 可得:
可得:![]()
则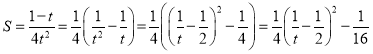 ,
,
![]()
![]() 故
故![]() 时,
时,![]() 即:
即:![]()
![]()
![]() 化简为:
化简为:![]() (
(![]() 为锐角)解得:
为锐角)解得: ![]()
综上所述:“蝴蝶形图案”面积的最小值为![]() ,取最小值时
,取最小值时![]() .
.

练习册系列答案
相关题目