题目内容
在平面直角坐标系xOy中,已知点M(0,3),直线l:x+y-4=0,点N(x,y)是圆C:x2+y2-2x-1=0上的动点,MA⊥l,NB⊥l,垂足分别为A、B,则线段AB的最大值为
3
| 2 |
3
.| 2 |
分析:由题意作出图象,结合题意可知当直线为m时会使得要求的距离最大,然后把问题转化为平行线AB与m间的距离公式即可求解.
解答: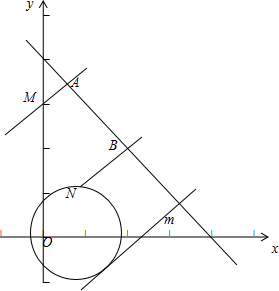 解:(如图)由题意可得:圆C的方程为(x-1)2+y2=2
解:(如图)由题意可得:圆C的方程为(x-1)2+y2=2
故圆C的圆心在(0,0)半径为
,
直线MA⊥l,故直线MA的斜率为1,过点M(0,3)
故直线MA的方程为:y=x+3,
由图象可知当动点N移动到直线为m是会使得AB最大,此时m与圆相切,
故可设m的方程为:y=x+b,故圆心到直线m的距离d=
=
,
解得d=-3,或d=-1(舍去)
故AB的距离为平行线MA与m的距离,由平行线间的距离公式可得AB=
=3
故答案为:3
 解:(如图)由题意可得:圆C的方程为(x-1)2+y2=2
解:(如图)由题意可得:圆C的方程为(x-1)2+y2=2故圆C的圆心在(0,0)半径为
| 2 |
直线MA⊥l,故直线MA的斜率为1,过点M(0,3)
故直线MA的方程为:y=x+3,
由图象可知当动点N移动到直线为m是会使得AB最大,此时m与圆相切,
故可设m的方程为:y=x+b,故圆心到直线m的距离d=
| |1+b| | ||
|
| 2 |
解得d=-3,或d=-1(舍去)
故AB的距离为平行线MA与m的距离,由平行线间的距离公式可得AB=
| |3-(-3)| | ||
|
| 2 |
故答案为:3
| 2 |
点评:本题为距离的最值得求解,涉及直线与圆的位置关系,点到直线的距离公式以及平行线间的距离,属中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是