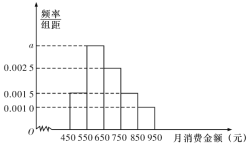
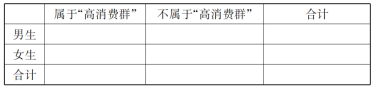
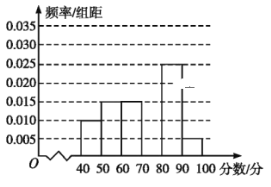
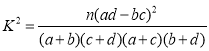题目内容
【题目】已知命题p：
在区间
上存在单调递减区间；命题q：函数
，且
有三个实根.若
为真命题，则实数
的取值范围是：（ ）
A.
B.
C.
D.
【答案】C
【解析】
根据命题p：
在区间
上存在单调递减区间，
转化为命题
：在区间上不存在单调递减区间，即
在区间上恒成立求解.根据
有三个实根，转化为
有三个实根求解，
为真命题，则两者取交集.
因为命题p：在区间上存在单调递减区间，
所以命题：在区间上不存在单调递减区间，
所以在区间上恒成立，
即
在区间上恒成立，
因为
在区间上是减函数，
所以
，
所以
.
所以命题：.
因为
，
所以
，
又因为有三个实根，
所以
有三个实根，
即有三个实根，
令
，
，
当
或
时，
，t是增函数，
当
时，
，t是减函数，
所以当
时，t取得最大值
，
当
时，t取得最小值
，
所以
.
若为真命题，则实数
的取值范围是：
.
故选：C
练习册系列答案
相关题目
【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中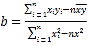
，
.）
