题目内容
【题目】某学校共有![]() 名学生,其中男生
名学生,其中男生![]() 人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了
人,为了解该校学生在学校的月消费情况,采取分层抽样随机抽取了![]() 名学生进行调查,月消费金额分布在
名学生进行调查,月消费金额分布在![]() 之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
之间.根据调查的结果绘制的学生在校月消费金额的频率分布直方图如图所示:
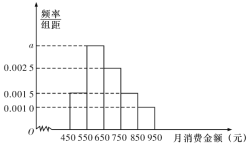
将月消费金额不低于![]() 元的学生称为“高消费群”.
元的学生称为“高消费群”.
(1)求![]() 的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
的值,并估计该校学生月消费金额的平均数(同一组中的数据用该组区间的中点值作代表);
(2)现采用分层抽样的方式从月消费金额落在![]() ,
,![]() 内的两组学生中抽取
内的两组学生中抽取![]() 人,再从这
人,再从这![]() 人中随机抽取
人中随机抽取![]() 人,记被抽取的
人,记被抽取的![]() 名学生中属于“高消费群”的学生人数为随机变量
名学生中属于“高消费群”的学生人数为随机变量![]() ,求
,求![]() 的分布列及数学期望;
的分布列及数学期望;
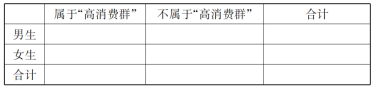
(3)若样本中属于“高消费群”的女生有![]() 人,完成下列
人,完成下列![]() 列联表,并判断是否有
列联表,并判断是否有![]() 的把握认为该校学生属于“高消费群”与“性别”有关?
的把握认为该校学生属于“高消费群”与“性别”有关?
(参考公式: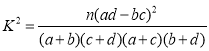 ,其中
,其中![]() )
)

【答案】(1)![]() ,平均数:
,平均数:![]() 元;(2)分布列见解析,
元;(2)分布列见解析,![]() ;(3)列联表见解析,有.
;(3)列联表见解析,有.
【解析】
(1)根据频率和为![]() ,列方程解出
,列方程解出![]() 的值,再由频率分布直方图求样本平均数,即可得解;
的值,再由频率分布直方图求样本平均数,即可得解;
(2)由题意可知随机变量![]() 服从超几何分布,确定
服从超几何分布,确定![]() 的取值,求出对应概率,可得
的取值,求出对应概率,可得![]() 的分布列,再计算数学期望即可;
的分布列,再计算数学期望即可;
(3)由题可知,样本中男生![]() 人,女生
人,女生![]() 人,属于“高消费群”的
人,属于“高消费群”的![]() 人,由此完成列联表,并由公式计算
人,由此完成列联表,并由公式计算![]() ,查表判断即可.
,查表判断即可.
(1)由题意知,![]() ,
,
解得![]() ,
,
样本的平均数为:
![]() (元),
(元),
所以估计该校学生月消费金额的平均数为![]() 元.
元.
(2)由题意,从![]() 中抽取
中抽取![]() 人,从
人,从![]() 中抽取
中抽取![]() 人.
人.
随机变量![]() 的所有可能取值有
的所有可能取值有![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() (
(![]() ),
),
所以,随机变量![]() 的分布列为
的分布列为
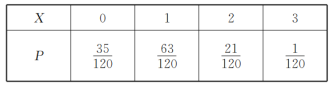
随机变量![]() 的数学期望
的数学期望![]() .
.
(3)由题可知,样本中男生![]() 人,女生
人,女生![]() 人,属于“高消费群”的
人,属于“高消费群”的![]() 人,其中女生
人,其中女生![]() 人;
人;
得出以下![]() 列联表:
列联表:

![]() ,
,
所以有![]() 的把握认为该校学生属于“高消费群”与“性别”有关.
的把握认为该校学生属于“高消费群”与“性别”有关.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目