题目内容
已知点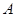 、
、 、
、 、
、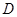 的坐标分别为
的坐标分别为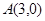 、
、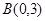 、
、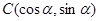 、
、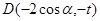 ,
,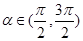
(1)若|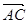 |=|
|=|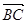 |,求角
|,求角 的值;
的值;
(2)若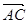 ·
·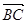 =
= ,求
,求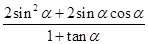 的值.
的值.
(3)若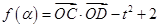 在定义域
在定义域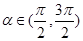 有最小值
有最小值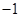 ,求
,求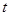 的值.
的值.
(1) ;(2)
;(2) ;(3)
;(3) .
.
解析试题分析:(1)根据已知A,B,C,D四点的坐标可以把 的坐标分别求得,即有
的坐标分别求得,即有 ,又根据
,又根据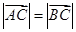 可以建立关于
可以建立关于 的方程,求得
的方程,求得 ,从而
,从而 ;(2)由平面向量数量积的坐标表示,
;(2)由平面向量数量积的坐标表示,
可得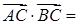
 ,化简可得
,化简可得 ,再将要求值的表达式化简为
,再将要求值的表达式化简为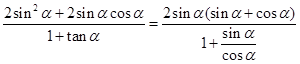
 ,
,
由 ,可求得
,可求得 ,从而需求值的表达式的值为
,从而需求值的表达式的值为 ;
;
(3)根据已知条件中点的坐标,可求得
 ,若令
,若令 ,则问题等价于当
,则问题等价于当 时,求使
时,求使 最小值为-1的
最小值为-1的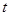 的值,显然
的值,显然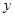 是关于
是关于 的开口向上的二次函数,若其在
的开口向上的二次函数,若其在 时,存在最小值,则必有对称轴
时,存在最小值,则必有对称轴 ,且当
,且当 时,
时,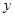 取到最小值-1,从而建立了关于
取到最小值-1,从而建立了关于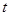 的方程,可解得
的方程,可解得 .
.
(1)又条件可得 ,又∵
,又∵ ,
,
∴  ,
,
由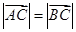 得
得 ,又
,又
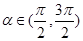 ,∴
,∴ 5分;
5分;
(2)由 ·
· =
= 得
得 ,
,
∴  ① 6分
① 6分
又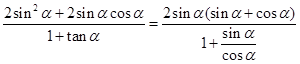
 7分
7分
由①式两边平方得 ∴
∴ 8分
8分
∴ . 9分;
. 9分;
依题意记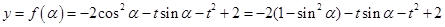
 10分
10分
令 ,
, (
( ,
,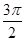 ),
), ,
,
则 11分
11分
关于 的二次函数开口向上,对称轴为
的二次函数开口向上,对称轴为 ,
, 在
在 上存在最小值,则对称轴
上存在最小值,则对称轴
 12分
12分
且当 时,
时, 取最小值为
取最小值为
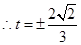 14分
14分
考点:1.平面向量的数

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
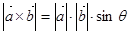 ,其中
,其中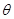 为向量
为向量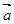 与
与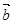 的夹角,若
的夹角,若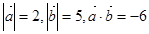 ,则
,则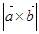 等于 .
等于 .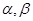 的始边为
的始边为 轴的非负半轴,点
轴的非负半轴,点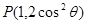 在角
在角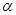 的终边上,点Q
的终边上,点Q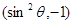 在角
在角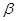 的终边上,且
的终边上,且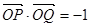 .
.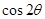 ;
; 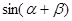 的值.
的值. 中,
中, ,
, ,设
,设 .
. 时,求
时,求 的值;
的值; ,求
,求 的值.
的值.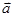 =(cos
=(cos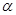 ,sin
,sin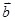 =(cos
=(cos ,sin
,sin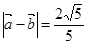 。
。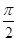 ,-
,-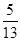 ,求sin
,求sin ,
, ,且
,且 .
. 的轨迹
的轨迹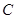 的方程;
的方程; 相交于不同的两点
相交于不同的两点 ,又点
,又点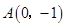 ,当
,当 时,求实数
时,求实数 的取值范围.
的取值范围.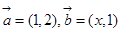
 为锐角,求
为锐角,求 的范围;
的范围;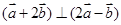 时,求
时,求
 ,
, ,求
,求
 ,若
,若 ,求
,求 的值.
的值. 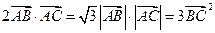 ,求角A、B、C的大小.
,求角A、B、C的大小.