题目内容
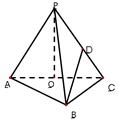
如图,已知矩形ABCD,M,N分别是AD,BC的中点,且AM=AB,将矩形沿MN折成直二面角,若P点是线段DN上一动点,求P到BM距离的最小值。
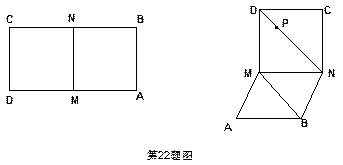
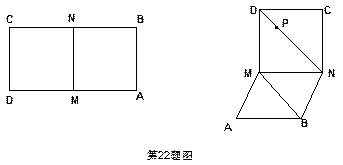
当点P位于距N点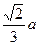 处时,P点到BM的距离取得最小值,这个最小值为
处时,P点到BM的距离取得最小值,这个最小值为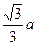 .
.
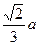 处时,P点到BM的距离取得最小值,这个最小值为
处时,P点到BM的距离取得最小值,这个最小值为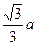 .
. 如图,过P点作PE⊥MN,垂足为E,过E点作EF⊥BM于F点,连结PF。
由题意可知平面CDMN⊥平面ABMN,∴PE⊥平面ABMN∴PF在平面ABMN中的射影为EF,由三垂线定理知PF⊥BM,即PF的长为P到BM的距离。
设AM=AB=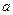 ,PN=
,PN=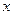 ,则
,则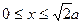 ∵四边形ABNM是正方形∴
∵四边形ABNM是正方形∴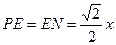 ,
,
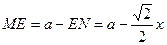 在Rt△EFM中
在Rt△EFM中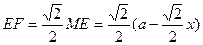
在Rt△EFP中,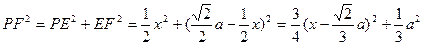
∴当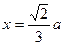 时,
时,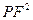 有最小值为
有最小值为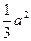 ,即当点P位于距N点
,即当点P位于距N点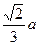 处时,P点到BM的距离取得最小值,这个最小值为
处时,P点到BM的距离取得最小值,这个最小值为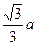 .
.

由题意可知平面CDMN⊥平面ABMN,∴PE⊥平面ABMN∴PF在平面ABMN中的射影为EF,由三垂线定理知PF⊥BM,即PF的长为P到BM的距离。
设AM=AB=
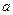 ,PN=
,PN=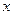 ,则
,则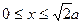 ∵四边形ABNM是正方形∴
∵四边形ABNM是正方形∴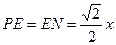 ,
,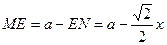 在Rt△EFM中
在Rt△EFM中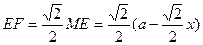
在Rt△EFP中,
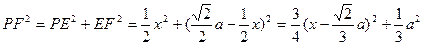
∴当
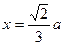 时,
时,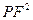 有最小值为
有最小值为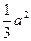 ,即当点P位于距N点
,即当点P位于距N点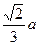 处时,P点到BM的距离取得最小值,这个最小值为
处时,P点到BM的距离取得最小值,这个最小值为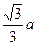 .
.

练习册系列答案
相关题目
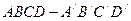 中
中
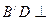 平面
平面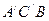 ;
;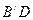 与平面
与平面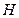 是
是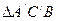 的重心(三角形三条中线的交点)
的重心(三角形三条中线的交点)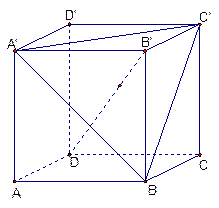
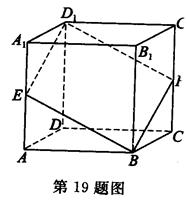
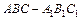 中,
中,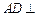 平面
平面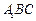 ,其垂足
,其垂足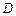 落在直线
落在直线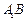 上.
上.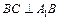 ;
;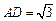 ,
,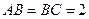 ,
,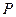 为
为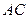 的中点,求三棱锥
的中点,求三棱锥 的体积.
的体积.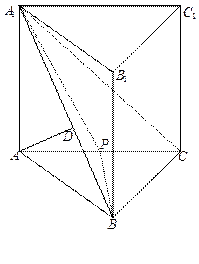
 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直, ,
,
 是线段
是线段 的中点.
的中点.
 ;(2)求二面角
;(2)求二面角 的大小;
的大小; 为一动点,若点
为一动点,若点
 ,求这一过程中形成的三棱锥
,求这一过程中形成的三棱锥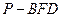 的体积的最小值.
的体积的最小值.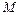 是
是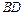 的中点.侧视图是直角梯形,俯视图是等腰直角
的中点.侧视图是直角梯形,俯视图是等腰直角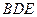 ?若存在,确定点N的位置;
?若存在,确定点N的位置;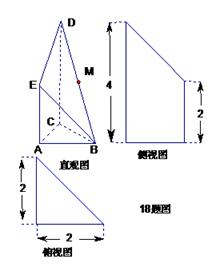
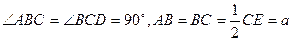 ,D是CE的中点,点M和点N在
,D是CE的中点,点M和点N在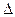 ADE绕AD向上翻折的过程中,分别以
ADE绕AD向上翻折的过程中,分别以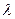 的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0
的速度,同时从点A和点B沿AE和BD各自匀速行进,t 为行进时间,0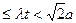 。
。
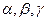 是三个不重合的平面,
是三个不重合的平面,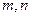 是不重合的直线,给出下列命题:
是不重合的直线,给出下列命题: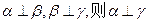 ;②若
;②若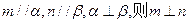 ;③若
;③若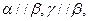 则
则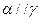 ;④若
;④若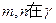 内的射影互相垂直,则
内的射影互相垂直,则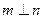 ,其中错误命题有 ( )
,其中错误命题有 ( )