Question

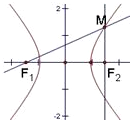双曲线

x2

a2

-

y2

b2

=1（a＞0，b＞0）的左、右焦点分别是F₁，F₂，过F₁作倾斜角为30°的直线交双曲线右支于M点，若MF₂垂直于x轴，则双曲线的离心率为（　　）

• A、

  6

• B、

  3

• C、

  2

• D、

  3

  3

Answer 1

分析：先在Rt△MF₁F₂中，利用∠MF₁F₂和F₁F₂求得MF₁和MF₂，进而根据双曲线的定义求得a，最后根据a和c求得离心率．

解答：解：如图在Rt△MF₁F₂中，∠MF₁F₂=30°，F₁F₂=2c
∴MF1=

2c

cos30°

=

4

3

3

c，MF2=2c•tan30°=

2

3

3

c
∴2a=MF1-MF2=

4

3

3

c-

2

3

3

c=

2

3

3

c
∴e=

c

a

=

3

，
故选B．

点评：本题主要考查了双曲线的简单性质，属基础题．