题目内容
若点O和点F(-2,0)分别是双曲线
-y2=1(a>0)的中心和左焦点,点P为双曲线右支上的任意一点,则
•
的取值范围为( )
| x2 |
| a2 |
| OP |
| FP |
A、[3-2
| ||
B、[3+2
| ||
C、[-
| ||
D、[
|
分析:先根据双曲线的焦点和方程中的b求得a,则双曲线的方程可得,设出点P,代入双曲线方程求得y0的表达式,根据P,F,O的坐标表示出
和
,进而求得
•
的表达式,利用二次函数的性质求得其最小值,则
•
的取值范围可得.
| OP |
| FP |
| OP |
| FP |
| OP |
| FP |
解答:解:因为F(-2,0)是已知双曲线的左焦点,
所以a2+1=4,即a2=3,所以双曲线方程为
-y2=1,
设点P(x0,y0),
则有
-y02=1(x0≥
),解得y02=
-1(x0≥
),
因为
=(x0+2,y0),
=(x0,y0),
所以
•
=x0(x0+2)+y02=x0(x0+2)+
-1=
+2x0-1,
此二次函数对应的抛物线的对称轴为x0=-
,
因为x0≥
,
所以当x0=
时,
•
取得最小值
×3+2
-1=3+2
,
故
•
的取值范围是[3+2
,+∞),
故选B.
所以a2+1=4,即a2=3,所以双曲线方程为
| x2 |
| 3 |
设点P(x0,y0),
则有
| x02 |
| 3 |
| 3 |
| x02 |
| 3 |
| 3 |
因为
| FP |
| OP |
所以
| OP |
| FP |
| x02 |
| 3 |
| 4x02 |
| 3 |
此二次函数对应的抛物线的对称轴为x0=-
| 3 |
| 4 |
因为x0≥
| 3 |
所以当x0=
| 3 |
| OP |
| FP |
| 4 |
| 3 |
| 3 |
| 3 |
故
| OP |
| FP |
| 3 |
故选B.
点评:本题考查待定系数法求双曲线方程,考查平面向量的数量积的坐标运算、二次函数的单调性与最值等,考查了同学们对基础知识的熟练程度以及知识的综合应用能力、运算能力.

练习册系列答案
相关题目
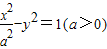 的中心和左焦点,点P为双曲线右支上的任意一点,则
的中心和左焦点,点P为双曲线右支上的任意一点,则 的取值范围为 .
的取值范围为 .