Question

【题目】已知定义域为R的奇函数f（x）满足：当x＞0时，f（x）=lnx，则函数g（x）=f（x）﹣sin4x的零点的个数为 ．

Answer 1

【答案】7
【解析】解：函数f（x）=sin4x是奇函数，且它的周期为 = ，
∵g（x）=f（x）﹣sin4x=0，
∴函数g（x）=f（x）﹣sin4x的零点的个数为
相当于f（x）=sin4x的零点个数，
即f（x）与sin4x的交点个数，
∴画出二者图象，由数形结合，
可知，在（﹣∞，0）有3个交点，0处有一个交点，（0，+∞）有3个交点，
故共有7个交点．
∴函数g（x）=f（x）﹣sin4x的零点的个数为7个，
所以答案是：7．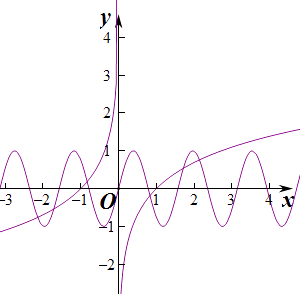

【考点精析】关于本题考查的函数奇偶性的性质，需要了解在公共定义域内，偶函数的加减乘除仍为偶函数；奇函数的加减仍为奇函数；奇数个奇函数的乘除认为奇函数；偶数个奇函数的乘除为偶函数；一奇一偶的乘积是奇函数;复合函数的奇偶性：一个为偶就为偶，两个为奇才为奇才能得出正确答案．