题目内容
20.已知函数f(x)=ln(x+m+1),m∈R.(I)若直线y=x+1与函数y=f(x)的图象相切,求m的值;
(Ⅱ)当m≤1时,求证f(x)<ex.
分析 (1)求出函数的导数,设出切点,求得切线的斜率,由点满足曲线和切线方程,解方程,可得m=1:
(2)由m≤1,可得ln(x+m+1)≤ln(x+2),要证f(x)<ex,只需证ln(x+2)<ex,令h(x)=ex-ln(x+2),求出导数,运用零点存在定理,可得?x0∈(-1,0),使h′(x0)=0,求得h(x)的最小值,证明它大于0,即可得证.
解答 解:函数f(x)=ln(x+m+1)的导数f′(x)=$\frac{1}{x+m+1}$,
(1)设直线y=x+1与函数f(x)的图象切于点(x0,y0),
则y0=x0+1,y0=ln(x0+m+1),$\frac{1}{{x}_{0}+m+1}$=1,
解得x0=-1,y0=0,m=1;
(2)证明:由m≤1,可得ln(x+m+1)≤ln(x+2),
要证f(x)<ex,只需证ln(x+2)<ex,
令h(x)=ex-ln(x+2),则h′(x)=ex-$\frac{1}{x+2}$,
由h′(-1)=$\frac{1}{e}$-1<0,h′(0)=$\frac{1}{2}$>0,
即有?x0∈(-1,0),使h′(x0)=0,
即${e}^{{x}_{0}}$=$\frac{1}{2+{x}_{0}}$,ln(x0+2)=-x0,
则h(x)在(-2,x0)上递减,在(x0,+∞)上递增,
即有h(x)min=h(x0)=${e}^{{x}_{0}}$-ln(x0+2),
则h(x)≥h(x)min=${e}^{{x}_{0}}$-ln(x0+2)=$\frac{1}{2+{x}_{0}}$+x0=$\frac{({x}_{0}+1)^{2}}{2+{x}_{0}}$>0,
则有f(x)<ex.
点评 本题考查导数的运用:求切线的斜率和求单调区间、极值和最值,主要考查导数的几何意义,函数的单调性的运用,考查运算能力,属于中档题.

 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案| A. | 1 | B. | $\frac{1}{2}$ | C. | -$\frac{1}{2}$ | D. | -1 |
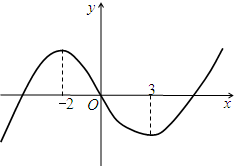
| A. | ($\frac{1}{2}$,+∞) | B. | (-∞,$\frac{1}{2}$) | C. | (-2,3) | D. | (-∞,-2) |
| A. | 12 | B. | 10 | C. | 8 | D. | 2+log35 |
| A. | y=sin2x | B. | y=cosx | C. | y=sin($\frac{π}{2}$-2x) | D. | y=tanx |
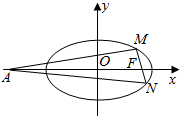 已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).
已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{6}}}{3}$,焦距为4,定点A(-4,0).