Question

【题目】设函数，，，若对任意成立，且数列满足：，.

（1）求函数的解析式；

（2）求证：；

（3）求证：.

Answer 1

【答案】（1）；（2）（证明略）；（3）（证明略）

【解析】

（1）由题令，解x=-1,所以-4≤f(-1)≤-4,则f(-1)=-4，得a=b-4，进而得对任意成立，由判别式整理解得b=2,即可得a=-2,则f(x)可求；（2）由得，进而，累乘得（3）由（2）得，累加得，再由证明数列递增，得则证得；欲证，即证,则需证，由，放缩归纳得，再证明即可

（1）由题对任意成立，

令，解x=-1,所以-4≤f(-1)≤-4,则f(-1)=-4

又，则f(-1)=a-b=-4，即a=b-4

所以对任意成立，即,则整理得∴b=2,则a=-2

所以

（2）由（1）知，，∴, ∴

,所以

又

（3）由（2）知

所以

所以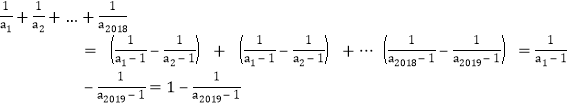

又,又,为递增数列，所以所以

由（2）可知，欲证，即证,则需证

∵,∴

所以

=

所以=2

因为2018<

所以,则>

所以证得，即证得

所以