题目内容
3. 如图.圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上-点.
如图.圆锥的轴截面SAB为等腰直角三角形,Q为底面圆周上-点.(1)若QB的中点为C,求证:平面SOC⊥平面SBQ.
(2)若∠AOQ=120°,QB=$\sqrt{3}$,求圆锥的表面积.
分析 (1)如图所示,由OB=OQ,QC=CB,利用等腰三角形的性质可得QB⊥OC.利用线面垂直的性质可得:BQ⊥SO.于是QB⊥平面SOC,可得QB⊥OH.再由线面垂直和面面垂直的判定定理,即可证明.
(2)由∠AOQ=120°,可得∠BOQ=60°.又QB=$\sqrt{3}$,可得OQ=$\sqrt{3}$.在等腰Rt△SAB中,AB=2$\sqrt{3}$,可得SA=SB=$\sqrt{6}$,代入圆锥表面积公式,可得答案.
解答 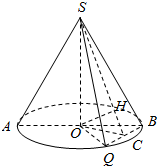 证明:(1)如图所示,
证明:(1)如图所示,
∵OB=OQ,QC=CB,
∴QB⊥OC,
又SO⊥底面OBQ,
∴BQ⊥SO.
又SO∩OC=O,
∴QB⊥平面SOC.
∴QB⊥OH.
又OH⊥SC,SC∩QB=C,
∴OH⊥平面SBQ.
又∵OH?平面SOC,
∴平面SOC⊥平面SBQ;
(2)解:∵∠AOQ=120°,
∴∠BOQ=60°.
又QB=$\sqrt{3}$,
∴OQ=$\sqrt{3}$.
在等腰Rt△SAB中,AB=2$\sqrt{3}$,
∴SA=SB=$\sqrt{6}$,
∴圆锥的表面积S=π×$\sqrt{3}×(\sqrt{3}+\sqrt{6)}$=(1+$\sqrt{2}$)3π.
点评 本题考查了等腰三角形的性质、直角三角形的性质、线面垂直和面面垂直的判定与性质定理、圆锥的表面积计算公式,考查了空间想象能力、推理能力与计算能力,属于中档题

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.长方体的一个顶点上三条棱长分别是3,4,5,且它的8个顶点都在同一球面上,则这个球的表面积是( )
| A. | 25π | B. | 125π | C. | 50π | D. | 以上都不对 |
8.已知α、β、γ是平面,a、b是直线,且α∩β=a,α⊥γ,β⊥γ,b?γ,则( )
| A. | a∥b | B. | a⊥b | ||
| C. | a与b相交 | D. | 不能确定a与b的关系 |
12.若f(x)=x2+3${∫}_{0}^{1}$f(x)dx,则${∫}_{0}^{1}$f(x)dx=( )
| A. | 4 | B. | -6 | C. | -$\frac{1}{6}$ | D. | $\frac{16}{3}$ |