题目内容
已知函数y=f(x)定义R上的奇函数,且x>0时,f(x)=x-1
(1)当x<0时,求f(x)的解析式
(2)画出y=|f(x)|在R上的图象,并由图象讨论m指出关于x的方程|f(x)|=m(m∈R)的根的个数(不需要说明理由).
(1)当x<0时,求f(x)的解析式
(2)画出y=|f(x)|在R上的图象,并由图象讨论m指出关于x的方程|f(x)|=m(m∈R)的根的个数(不需要说明理由).
分析:(1)当x<0时,-x>0,结合当x>0时,f(x)=x-1可求出当x<0时f(x)的解析式
(2)由(1)中和已知中函数的解析式,结合定义在R上的奇函数图象必过原点,及函数图象的对折变换,可画出y=|f(x)|在R上的图象,结合图象可分析出关于x的方程|f(x)|=m(m∈R)的根的个数.
(2)由(1)中和已知中函数的解析式,结合定义在R上的奇函数图象必过原点,及函数图象的对折变换,可画出y=|f(x)|在R上的图象,结合图象可分析出关于x的方程|f(x)|=m(m∈R)的根的个数.
解答:解:(1)设x<0,则-x>0
∵x>0时,f(x)=x-1
∴f(-x)=-x-1
∵函数y=f(x)定义R上的奇函数
∴f(x)=-f(-x)=x+1
(2)∴f(x)=
,
其图象如图所示
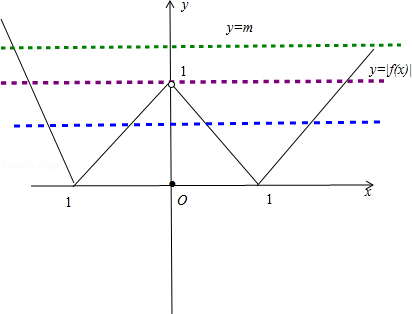
结合函数的图象可知,
①当m≥1时,方程有2个根
②m=0时,有3个根
③0<m<1时,有4个根
④m<0时,没有根
∵x>0时,f(x)=x-1
∴f(-x)=-x-1
∵函数y=f(x)定义R上的奇函数
∴f(x)=-f(-x)=x+1
(2)∴f(x)=
|
其图象如图所示

结合函数的图象可知,
①当m≥1时,方程有2个根
②m=0时,有3个根
③0<m<1时,有4个根
④m<0时,没有根
点评:本题考查的知识点是函数图象的作法,函数解析式的求法,利用图象法求方程的根,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目
 已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为
已知函数y=f(x)是定义在R上的奇函数,当x>0 时,f(x)的图象如图所示,则不等式x[f(x)-f(-x)]≤0 的解集为 已知函数y=f(x)的图象如图,则满足
已知函数y=f(x)的图象如图,则满足