题目内容

2．已知函数f（x）=x3+（1-a）x2-a（a+2）x+b（a，b∈R）．若函数f（x）的图象过原点，且在原点处的切线斜率是-3，求a，b的值．

分析 根据函数过原点，先求出b，然后求函数的导数，利用f′（0）=-3，解方程即可．

解答 解：∵函数f（x）的图象过原点，
∴f（0）=0，即f（0）=b=0，
函数的导数f′（x）=3x2+2（1-a）x-a（a+2），
∵函数f（x）在原点处的切线斜率是-3，
则f′（0）=-3，
即-a（a+2）=-3，
则a2+2a-3=0，
解得a=1或a=-3，
故a=1或a=-3，b=0．

点评 本题主要考查导数的计算以及导数的几何意义，求函数的导数，建立方程关系是解决本题的关键．

练习册系列答案
相关题目
11．若函数y=sin（ωx+$\frac{5π}{3}$）（ω＞0）的最小正周期是$\frac{π}{3}$，则ω=6．
13．已知抛物线y=$\frac{1}{8}$x2与双曲线$\frac{{y}^{2}}{{a}^{2}}$-x2=1（a＞0）有共同的焦点F，O为坐标原点，P在x轴上方且在双曲线上，则$\overrightarrow{OP}$•$\overrightarrow{FP}$的最小值为3-2$\sqrt{3}$．．
10．函数f（x）=$\frac{1}{3}$x3-x2+1是减函数的区间为（　　）
A．（2，+∞）B．（-∞，2）C．（-∞，0）D．（0，2）
17．已知等比数列{an}的前n项和为Sn，若Sm=5，S2m=20，则S3m=65．
7．已知$\overrightarrow a$，$\overrightarrow b$是同一平面内的两个向量，其中$|{\overrightarrow a}|=1，|{\overrightarrow b}|=2，\overrightarrow a•\overrightarrow b=-\sqrt{3}$．
（1）求$\overrightarrow a$与$\overrightarrow b$的夹角θ； 
（2）求|$\overrightarrow a$-$\sqrt{3}$$\overrightarrow b$|的值．
14．不等式组$\left\{\begin{array}{l}{y≤x+5}\\{x+y≥0}\\{x-1≤0}\end{array}\right.$所表示的平面区域内有36个整点．
11．已知函数f（x）=（1-|x|）（x+2）．
（1）写出该函数的大致图象；
（2）写出该函数的定义域、值域和单调区间．
12．如图所示，程序执行后的输出结果为（　　）
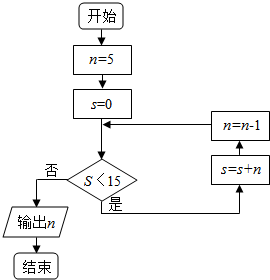
A．0B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网