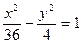题目内容
(本题满分12分)已知点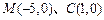 ,
,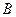 分
分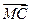 所成的比为2,
所成的比为2,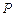 是平面上一动点,且满足
是平面上一动点,且满足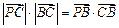 .(1)求点
.(1)求点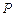 的轨迹
的轨迹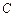 对应的方程;(2) 已知点
对应的方程;(2) 已知点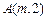 在曲线
在曲线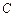 上,过点
上,过点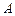 作曲线
作曲线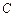 的两条弦
的两条弦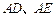 ,且直线
,且直线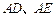 的斜率
的斜率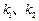 满足
满足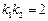 ,试推断:动直线
,试推断:动直线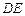 有何变化规律,证明你的结论.
有何变化规律,证明你的结论.
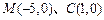 ,
,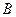 分
分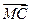 所成的比为2,
所成的比为2,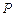 是平面上一动点,且满足
是平面上一动点,且满足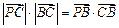 .(1)求点
.(1)求点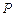 的轨迹
的轨迹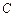 对应的方程;(2) 已知点
对应的方程;(2) 已知点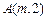 在曲线
在曲线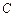 上,过点
上,过点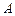 作曲线
作曲线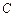 的两条弦
的两条弦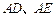 ,且直线
,且直线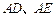 的斜率
的斜率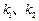 满足
满足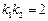 ,试推断:动直线
,试推断:动直线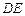 有何变化规律,证明你的结论.
有何变化规律,证明你的结论.(Ⅰ)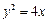 (Ⅱ)
(Ⅱ) 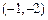
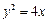 (Ⅱ)
(Ⅱ) 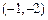
(1)因为点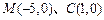 ,
,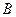 分
分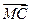 所成的比为2,所以
所成的比为2,所以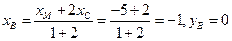 2分设
2分设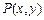 代入
代入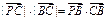 ,得
,得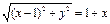 .化简得
.化简得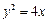 .……4分
.……4分
(2)将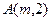 代入
代入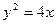 ,得
,得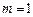 ,即
,即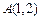 .…5分
.…5分
∵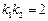 ,
,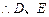 两点不可能关于
两点不可能关于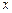 轴对称,∴
轴对称,∴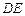 的斜率必存在.…6分
的斜率必存在.…6分
设直线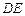 的方程为
的方程为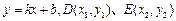 由
由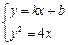 得
得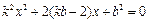 .
.
∵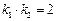 ,∴
,∴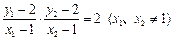 .且
.且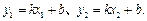
∴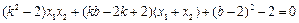 .
.
将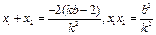 代入化简得
代入化简得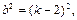 ∴
∴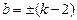 .……10分
.……10分
(i)将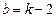 代入
代入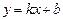 得
得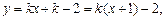 过定点
过定点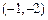 .
.
(ii)将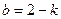 入
入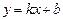 得
得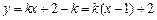 .过定点
.过定点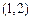 .即为
.即为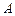 点,不合题意,舍去.
点,不合题意,舍去.
∴直线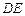 恒过定点
恒过定点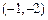 .……12分
.……12分
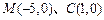 ,
,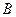 分
分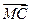 所成的比为2,所以
所成的比为2,所以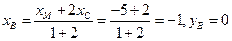 2分设
2分设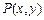 代入
代入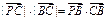 ,得
,得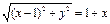 .化简得
.化简得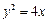 .……4分
.……4分(2)将
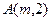 代入
代入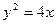 ,得
,得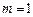 ,即
,即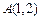 .…5分
.…5分∵
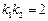 ,
,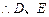 两点不可能关于
两点不可能关于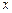 轴对称,∴
轴对称,∴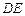 的斜率必存在.…6分
的斜率必存在.…6分设直线
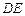 的方程为
的方程为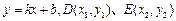 由
由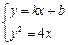 得
得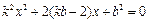 .
.∵
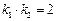 ,∴
,∴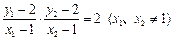 .且
.且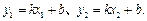
∴
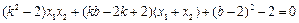 .
.将
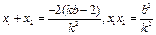 代入化简得
代入化简得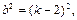 ∴
∴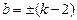 .……10分
.……10分(i)将
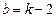 代入
代入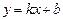 得
得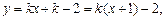 过定点
过定点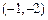 .
.(ii)将
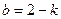 入
入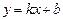 得
得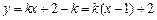 .过定点
.过定点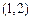 .即为
.即为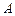 点,不合题意,舍去.
点,不合题意,舍去.∴直线
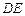 恒过定点
恒过定点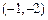 .……12分
.……12分
练习册系列答案
相关题目
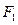 ,
,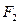 为椭圆
为椭圆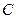 :
: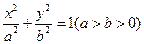 的左、右两个焦点,直线
的左、右两个焦点,直线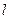 :
: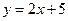 与椭圆
与椭圆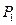 ,
,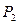 ,已知椭圆中心
,已知椭圆中心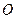 点关于
点关于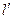 上.
上.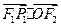 ,
, ,
, 成等差数列,求椭圆
成等差数列,求椭圆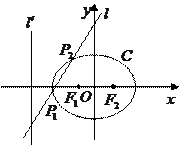
 的坐标为
的坐标为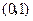 ,直线
,直线 的方程为
的方程为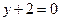 ,动点
,动点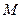 到点
到点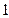 ,求动点
,求动点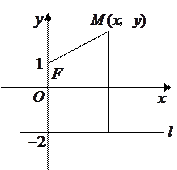
 ,
,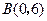 ,
,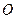 为原点.
为原点.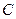 在线段
在线段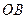 上,且
上,且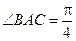 ,求
,求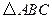 的面积;
的面积;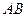 的对称点为
的对称点为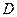 ,延长
,延长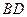 到
到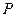 ,且
,且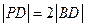 ,已知直线
,已知直线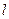 :
: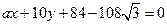 经过点
经过点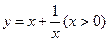 交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。
交于两个不同点M和N。求曲线C在点M、N处切线的交点轨迹。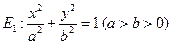 的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点
的一条弦,M(2,1)是AB的中点,以M为焦点且以椭圆E1的右准线为相应准线的双曲线E2与直线AB交于点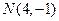 . (1)设双曲线E2的离心率为
. (1)设双曲线E2的离心率为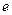 ,求
,求 的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.
的函数表达式; (2)当椭圆E1与双曲线E2的离心率互为倒数时,求椭圆E1的方程.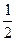 )为方向向量的直线l过点(0,
)为方向向量的直线l过点(0, 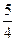 ),抛物线C:
),抛物线C: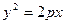 (p>0)的顶点关于直线l的对称点在该抛物线上.
(p>0)的顶点关于直线l的对称点在该抛物线上.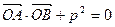 (O为原点,A、B异于原点),试求点N的轨迹方程.
(O为原点,A、B异于原点),试求点N的轨迹方程.