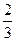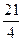题目内容
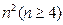 个正数排成
个正数排成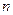 行
行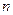 列:
列: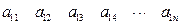
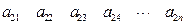
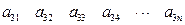

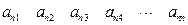
其中每一行的数由左至右成等差数列,每一列的数由上至下成等比数列,并且所有公比相等,已知
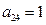 ,
,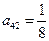 ,
,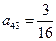 ,试求
,试求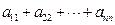 的值.(本题满分13分)
的值.(本题满分13分)解:设 ,第一行数的公差为
,第一行数的公差为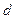 ,第一列数的公比为
,第一列数的公比为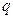 ,可得
,可得
又设第一行数列公差为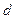 ,各列数列的公比为
,各列数列的公比为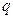 ,则第四行数列公差是
,则第四行数列公差是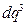 ,于是可得
,于是可得
 .………………….…. (3分)
.………………….…. (3分)
解此方程组,得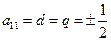 ,由于给
,由于给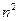 个数都是正数,必有
个数都是正数,必有 ,从而有
,从而有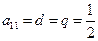 , .………………………. (4分)
, .………………………. (4分)
于是对任意的 ,有
,有 …….…… (6分)
…….…… (6分)
得 , …………………. (8分)
, …………………. (8分)
又 . …………………. (10分)
. …………………. (10分)
两式相减后得: . …………… (12分)
. …………… (12分)
所以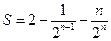 …………………. (13分)
…………………. (13分)
 ,第一行数的公差为
,第一行数的公差为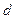 ,第一列数的公比为
,第一列数的公比为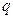 ,可得
,可得
又设第一行数列公差为
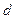 ,各列数列的公比为
,各列数列的公比为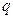 ,则第四行数列公差是
,则第四行数列公差是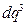 ,于是可得
,于是可得 .………………….…. (3分)
.………………….…. (3分)解此方程组,得
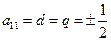 ,由于给
,由于给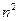 个数都是正数,必有
个数都是正数,必有 ,从而有
,从而有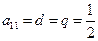 , .………………………. (4分)
, .………………………. (4分)于是对任意的
 ,有
,有 …….…… (6分)
…….…… (6分)得
 , …………………. (8分)
, …………………. (8分)又
 . …………………. (10分)
. …………………. (10分)两式相减后得:
 . …………… (12分)
. …………… (12分)所以
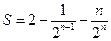 …………………. (13分)
…………………. (13分) 略

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
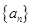 满足
满足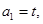 ,
,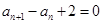
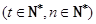 ,记数列
,记数列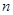 项和的最大值为
项和的最大值为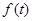 ,则
,则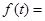 .
.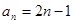
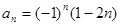
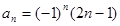
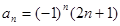
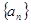 中,已知
中,已知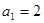 ,
,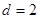 ,则第
,则第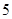 项
项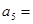 ★
★  的前
的前 项和为
项和为 ,若
,若 ,
,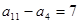 , 则
, 则 等于( )
等于( )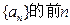 项和为
项和为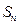 ,若m>1,
,若m>1,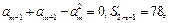 则m=_____。
则m=_____。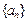 的首项
的首项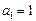 ,公差
,公差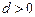 .且
.且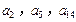 分别是等比数列
分别是等比数列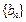 的
的
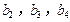 .
. 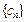 对任意自然数
对任意自然数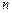 均有:
均有: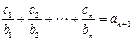 成立.求
成立.求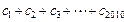 的值。
的值。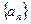 的前
的前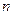 项和为
项和为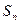 ,若
,若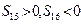 ,则
,则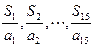 中最大的是 .
中最大的是 . 个等差数列{
个等差数列{ 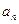 }和{
}和{ 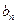 }的前n项和分别是
}的前n项和分别是 ,己知
,己知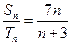 ,则
,则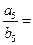 ()
()