题目内容
在平面直角坐标系xOy中,直角三角形ABC的三个顶点都在椭圆
+y2=1(a>1)上,其中A(0,1)为直角顶点.若该三角形的面积的最大值为
,则实数a的值为
| x2 |
| a2 |
| 27 |
| 8 |
3
3
.分析:设直线AB的方程为y=kx+1,(k≠0).将直线AB方程与椭圆消去y,解得B的坐标,再用两点之间距离公式,可以算出AB长关于a、k的表达式,同理可得AC长关于a、k的表达式,从而得到Rt△ABC的面积S关于a、k的表达式,根据基本不等式进行讨论,可得△ABC的面积S的最大值为
,最后结合题意解关于a的方程,即可得到实数a的值.
| a4 |
| a(a2-1) |
解答: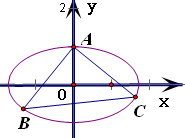 解:设直线AB的方程为y=kx+1则直线AC的方程可设为y=-
解:设直线AB的方程为y=kx+1则直线AC的方程可设为y=-
x+1,(k≠0)
由
消去y,得(1+a2k2)x2+2a2kx=0,所以x=0或x=
∵A的坐标(0,1),
∴B的坐标为(
,k•
+1),即B(
,
)
因此,AB=
=
•
,
同理可得:AC=
•
∴Rt△ABC的面积为S=
AB•AC=
•
=
令t=|k+
|,得S=
=
∵t=|k+
|≥2,∴S△ABC≤
=
当且仅当
=a
,即t=
时,△ABC的面积S有最大值为
=
解之得a=3或a=
∵a=
时,t=
<2不符合题意,
∴a=3
故答案为:3
 解:设直线AB的方程为y=kx+1则直线AC的方程可设为y=-
解:设直线AB的方程为y=kx+1则直线AC的方程可设为y=-| 1 |
| k |
由
|
| -2a2k |
| 1+a2k2 |
∵A的坐标(0,1),
∴B的坐标为(
| -2a2k |
| 1+a2k2 |
| -2a2k |
| 1+a2k2 |
| -2a2k |
| 1+a2k2 |
| 1-a2k2 |
| 1+a2k2 |
因此,AB=
(0-
|
| 1+k2 |
| |2a2k| |
| 1+a2k2 |
同理可得:AC=
1+
|
|
| ||
1+
|
∴Rt△ABC的面积为S=
| 1 |
| 2 |
2+k2+
|
| 2a4 | ||
1+a4+a2(k2+
|
2a4|k+
| ||
1+a4+a2(k2+
|
令t=|k+
| 1 |
| k |
| 2a4t |
| 1+a4+a2(t2-2) |
| 2a4 | ||
|
∵t=|k+
| 1 |
| k |
| 2a4 | ||||
2
|
| a4 |
| a(a2-1) |
当且仅当
| a2-1 | ||
|
| t |
| a2-1 |
| a |
| a4 |
| a(a2-1) |
| 27 |
| 8 |
解之得a=3或a=
3+
| ||
| 16 |
∵a=
3+
| ||
| 16 |
| a2-1 |
| a |
∴a=3
故答案为:3
点评:本题在椭圆上求内接直角三角形面积的最大值问题,着重考查了椭圆的简单几何性质和利用基本不等式讨论函数的最值等知识,属于中档题.

练习册系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是