题目内容
( 本小题共13分)
本小题共13分)
某学校高一年级开设了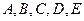 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量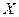 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加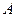 课程的人数,求
课程的人数,求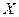 的分布列与数学期望.
的分布列与数学期望.
 本小题共13分)
本小题共13分)某学校高一年级开设了
 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量
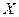 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加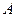 课程的人数,求
课程的人数,求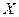 的分布列与数学期望.
的分布列与数学期望.(Ⅰ)125(Ⅱ)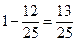 (Ⅲ)见解析
(Ⅲ)见解析
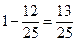 (Ⅲ)见解析
(Ⅲ)见解析(Ⅰ)甲、乙、丙三名学生每人选择五门选修课的方法数是5种,
故共有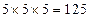 (种).
(种).
(Ⅱ)三名学生选择三门不同选修课程的概率为: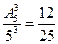 .
.
∴三名学生中至少有两人选修同一门课程的概率为: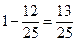 .
.
(Ⅲ)由题意: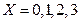 .
.
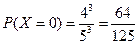 ;
; 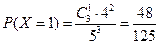 ;
;
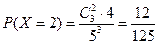 ;
; 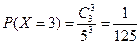 .
.

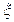 的分布列为
的分布列为

数学期望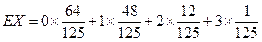 =
=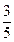 .----------------13分
.----------------13分
故共有
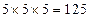 (种).
(种).(Ⅱ)三名学生选择三门不同选修课程的概率为:
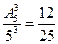 .
.∴三名学生中至少有两人选修同一门课程的概率为:
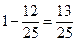 .
.(Ⅲ)由题意:
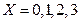 .
.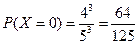 ;
; 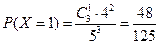 ;
;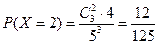 ;
; 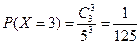 .
.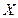 | 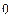 | 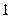 | 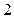 | 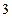 |
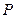 | 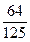 | 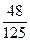 | 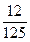 | 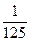 |

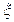 的分布列为
的分布列为
数学期望
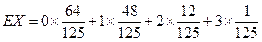 =
=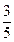 .----------------13分
.----------------13分
练习册系列答案
相关题目
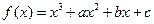 在
在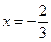 与
与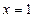 时都取得极值.
时都取得极值.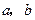 的值 (2)求函数
的值 (2)求函数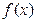 的单调区间;
的单调区间; 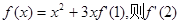 = ( )
= ( )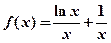 .
.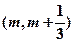 (其中
(其中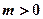 )上存在极值,求实数
)上存在极值,求实数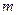 的取值范围;
的取值范围;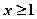 时,不等式
时,不等式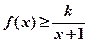 恒成立,求实数
恒成立,求实数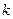 的取值范围;
的取值范围;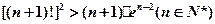 .
.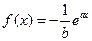 的图像在
的图像在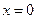 处的切线
处的切线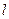 与圆
与圆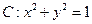 相离,则点
相离,则点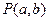 与圆
与圆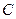 的位置关系是 .
的位置关系是 .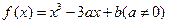 在点
在点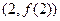 处与直线
处与直线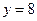 相切,则双曲线
相切,则双曲线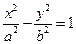 的离心率等于 .
的离心率等于 .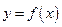 的导函数
的导函数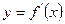 的图像如图所示,则
的图像如图所示,则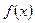 的解析式可能是( )
的解析式可能是( )
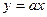
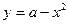
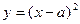
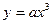
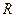 上的函数
上的函数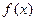 满足
满足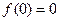 ,
,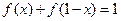 ,
,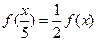 ,且当
,且当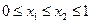 时,有
时,有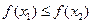 ,则
,则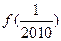 的值为( )
的值为( )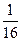
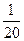
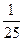
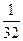
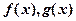 都是定义在
都是定义在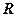 上的函数,并满足以下条件:
上的函数,并满足以下条件: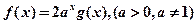 ;(2)
;(2)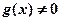 ;(3)
;(3)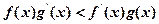
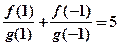 ,则
,则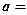 ( )
( )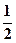
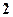
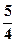

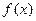 是定义在R上的奇函数,
是定义在R上的奇函数,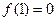 ,
,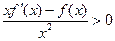
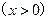 ,则不等式
,则不等式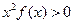 的解集是 .
的解集是 .