题目内容
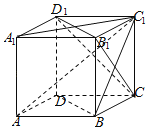
【题目】如图，在正方体ABCD－A1B1C1D1中，有下面结论：
①AC∥平面CB1D1；
②AC1⊥平面CB1D1；
③AC1与底面ABCD所成角的正切值是
；
④AD1与BD为异面直线.其中正确的结论的序号是________.
【答案】②③④
【解析】
利用线面平行，线面垂直和线面所成角的定义分别判断．①因为AC∩平面CB1D1=C，所以AC∥平面CB1D1错误；根据线面垂直的判定定理得到②正确；由线面角的定义得到AC1在底面ABCD的射影为AC，所以∠C1AC是AC1与底面ABCD所成的角，在三角形中求得正切值③正确；由异面直线的定义可知，AD1与BD为异面直线，所以④正确．
①因为AC∩平面CB1D1=C，所以AC∥平面CB1D1错误，所以①错误．
②连结BC1，A1 C1，则BC1⊥B1 C，又因为AB⊥面BC C1B1
故 AB⊥B1 C, AB∩BC1=B，故B1 C⊥面ABC1
进而得到AC1⊥B1C，
连接A1 C1，同理可证B1D1⊥AC1
又因为B1D1∩B1 C于点B1
故得到AC1⊥平面CB1D1
所以②正确．
③因为AC1在底面ABCD的射影为AC，所以∠C1AC是AC1与底面ABCD所成的角，设正方体的边长为a,则AC=
所以
所以③正确．
④由异面直线的定义可知，AD1与BD为异面直线，所以④正确．
故答案为：②③④．
练习册系列答案
阅读快车系列答案
相关题目
