题目内容
【题目】函数y=﹣sin（ωx+φ）（ω＞0，φ∈（﹣ 
， ））的一条对称轴为x= 
，一个对称中心为（ 
，0），在区间[0， ]上单调．
（1）求ω，φ的值；
（2）用描点法作出y=sin（ωx+φ）在[0，π]上的图象．
【答案】
（1）解：由题意得：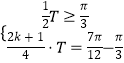 
，即 
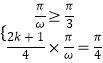，解得 
又ω＞0，k∈Z，所以ω=2，
x= 
为对称轴，2× 
+φ=kπ+ 
，所以φ=kπ﹣ 
，
又φ∈（﹣ ， ），
∴φ=﹣
（2）解：由（1）可知f（x）=sin（2x﹣ ），
由x∈[0，π]，
所以2x﹣ ∈[﹣ ， 
]，
列表：
2x﹣ | ﹣ | 0 |
| π |
|
|
x | 0 |
|
|
|
| π |
f（x） | ﹣ | 0 | 1 | 0 | ﹣1 |
|
画图：
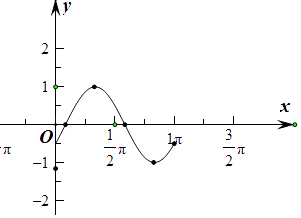
【解析】（1）由条件利用三角形函数的周期，对称轴，对称中心，即可ω，φ．（2）用五点法作函数y=Asin（ωx+φ）在一个周期[0，π]上的图象．
【考点精析】解答此题的关键在于理解五点法作函数y=Asin（ωx+φ）的图象的相关知识，掌握描点法及其特例—五点作图法（正、余弦曲线），三点二线作图法（正、余切曲线）．
练习册系列答案
相关题目
