题目内容
(2013•惠州一模)已知f(x)=lnx,g(x)=
x3+
x2+mx+n,直线l与函数f(x),g(x)的图象都相切于点(1,0).
(1)求直线l的方程及g(x)的解析式;
(2)若h(x)=f(x)-g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的极大值.
| 1 |
| 3 |
| 1 |
| 2 |
(1)求直线l的方程及g(x)的解析式;
(2)若h(x)=f(x)-g′(x)(其中g′(x)是g(x)的导函数),求函数h(x)的极大值.
分析:(1)先确定直线l的方程为y=x-1,利用直线l与g(x)的图象相切,且切于点(1,0),建立方程,即可求得g(x)的解析式;
(2)确定函数h(x)的解析式,利用导数求得函数的单调性,即可求函数h(x)的极大值.
(2)确定函数h(x)的解析式,利用导数求得函数的单调性,即可求函数h(x)的极大值.
解答:解:(1)直线l是函数f(x)=lnx在点(1,0)处的切线,故其斜率k=f′(1)=1,
∴直线l的方程为y=x-1.…(2分)
又因为直线l与g(x)的图象相切,且切于点(1,0),
∴g(x)=
x3+
x2+mx+n在点(1,0)的导函数值为1.
∴
,∴
,…(4分)
∴g(x)=
x3+
x2-x+
…(6分)
(2)∵h(x)=f(x)-g′(x)=lnx-x2-x+1(x>0)…(7分)
∴h′(x)=
-2x-1=
=-
…(9分)
令h′(x)=0,得x=
或x=-1(舍)…(10分)
当0<x<
时,h′(x)>0,h(x)递增;当x>
时,h′(x)<0,h(x)递减…(12分)
因此,当x=
时,h(x)取得极大值,
∴[h(x)]极大=h(
)=ln
+
…(14分)
∴直线l的方程为y=x-1.…(2分)
又因为直线l与g(x)的图象相切,且切于点(1,0),
∴g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
∴
|
|
∴g(x)=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 6 |
(2)∵h(x)=f(x)-g′(x)=lnx-x2-x+1(x>0)…(7分)
∴h′(x)=
| 1 |
| x |
| 1-2x2-x |
| x |
| (2x-1)(x+1) |
| x |
令h′(x)=0,得x=
| 1 |
| 2 |
当0<x<
| 1 |
| 2 |
| 1 |
| 2 |
因此,当x=
| 1 |
| 2 |
∴[h(x)]极大=h(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
点评:本题考查导数知识的运用,考查切线方程,考查函数的单调性与极值,考查学生的计算能力,正确求导是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
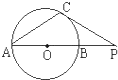 (2013•惠州一模)(几何证明选做题)
(2013•惠州一模)(几何证明选做题)