题目内容
（2013•惠州一模）若集合A={x|x2-4x-5=0}，B={x|x2=1}，则A∩B=（ ）
分析：分别求出集合A和B中一元二次方程的解，确定出两集合，找出两集合的公共元素，即可求出两集合的交集．
解答：解：由集合A中的方程x2-4x-5=0，
变形得：（x-5）（x+1）=0，
解得：x=5或x=-1，
∴集合A={-1，5}，
由集合B中的方程x2=1，
解得：x=1或x=-1，
∴集合B={-1，1}，
则A∩B={-1}．
故选B
变形得：（x-5）（x+1）=0，
解得：x=5或x=-1，
∴集合A={-1，5}，
由集合B中的方程x2=1，
解得：x=1或x=-1，
∴集合B={-1，1}，
则A∩B={-1}．
故选B
点评：此题属于以一元二次方程的解法为平台，考查了交集及其运算，是高考中常考的基本题型．
练习册系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
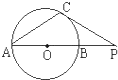（2013•惠州一模）（几何证明选做题）