题目内容
10.已知f(x)=x2+2ax+2,x∈R.(Ⅰ)若函数F(x)=f[f(x)]与f(x)在x∈R时有相同的值域,求a的取值范围.
(Ⅱ)若方程f(x)+|x2-1|=2在(0,2)上有两个不同的根α,β,求a的取值范围,并证明$\frac{1}{α}+\frac{1}{β}$<4.
分析 (Ⅰ)利用二次函数的对称轴和值域的关系寻找解决问题的突破口,关键要理解f[f(x)]与f(x)在x∈R时有相同的值域等价于
f(x)的最小值要小于二次函数顶点的横坐标;
(Ⅱ)将绝对值符号去掉进行讨论是解决本题的关键,利用方程根与系数的关系,进行放缩求解转化是证明本题的关键.
解答 解:(Ⅰ)当x∈R时,函数f(x)=x2+2ax+2的图象是开口向上,
且对称轴为x=-a的抛物线,f(x)的值域为[2-a2,+∞),
所以F(x)=f[f(x)]的值域也为[2-a2,+∞)的充要条件
是2-a2≤-a,即a2-a-2≥0,
∴a≤-1,或a≥2,
即a的取值范围为(-∞,-1]∪[2,+∞)
证明:(Ⅱ)f(x)+|x2-1|=2,即x2+2ax+|x2-1|=0,由分析知a≠0
不妨设0<α<β<2,令H(x)=x2+2ax+|x2-1|=$\left\{\begin{array}{l}2ax+1,\left|x\right|≤1\\ 2{x}^{2}+2ax-1,\left|x\right|>1\end{array}\right.$
因为H(x)在(0,1]上是单调函数,所以H(x)=0在(0,1]上至多有一个解.
若α,β∈(1,2),即α,β就是2x2+2ax-1=0的解,αβ=-$\frac{1}{2}$<0,与题设矛盾.
因此,α∈(0,1],β∈(1,2).由H(α)=0得a=-$\frac{1}{2α}$,所以a≤-$\frac{1}{2}$;
由H(β)=0得a=$\frac{1}{2β}-β$,所以-$\frac{7}{4}$<a<-$\frac{1}{2}$.
故当-$\frac{7}{4}$<a<-$\frac{1}{2}$时,方程f(x)+|x2-1|=2在(0,2)上有两个解.
由a=-$\frac{1}{2α}$和a=$\frac{1}{2β}-β$消去a,得 $\frac{1}{α}+\frac{1}{β}$=2β.
由β∈(1,2),得$\frac{1}{α}+\frac{1}{β}$<4.
点评 本题考查复合函数的知识,考查二次函数的值域意识,考查方程的根与方程系数之间的关系,求取值范围关键要确定出字母满足的不等式.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| 1 | 2 | ( ) | ( ) | ( ) | … | a1j | … |
| 3 | 6 | ( ) | ( ) | ( ) | … | a2j | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | a3j | … |
| ai1 | ai2 | ai3 | ai4 | ai5 | … | aij | … |
| ( ) | ( ) | ( ) | ( ) | ( ) | … | … | … |
表示第i行第j列的数.
(1)写出a34的值并求出aij的计算公式;
(2)若数列{bn}满足bn=a2n+log2a2n,求数列{bn}的前n项和Sn.
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
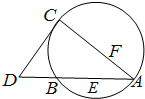 如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.
如图,CD为△ABC外接圆的切线,E,F分别为弦AB与弦AC上的点,AB的延长线交直线CD于点D,且BC•AE=DC•AF,B,E,F,C四点共圆.