题目内容
(本小题13分)已知函数 与
与 的图象相交于
的图象相交于 ,
, ,
, ,
, 分别是
分别是 的图象在
的图象在 两点的切线,
两点的切线, 分别是
分别是 ,
, 与
与 轴的交点.
轴的交点.
(1)求 的取值范围;
的取值范围;
(2)设 为点
为点 的横坐标,当
的横坐标,当 时,写出
时,写出 以
以 为自变量的函数式,并求其定义域和值域;
为自变量的函数式,并求其定义域和值域;
(3)试比较 与
与 的大小,并说明理由(
的大小,并说明理由( 是坐标原点).
是坐标原点).
解:(Ⅰ)由方程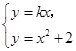 消
消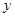 得
得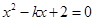 .①
.①
依题意,该方程有两个正实根,故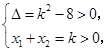 解得
解得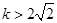 .
.
(Ⅱ)由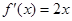 ,求得切线
,求得切线 的方程为
的方程为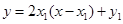 ,
,
由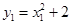 ,并令
,并令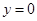 ,得
,得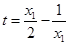
 ,
,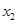 是方程①的两实根,且
是方程①的两实根,且 ,故
,故 ,
,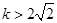 ,
, 是关于
是关于 的减函数,所以
的减函数,所以 的取值范围是
的取值范围是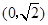 .
. 是关于
是关于 的增函数,定义域为
的增函数,定义域为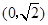 ,所以值域为
,所以值域为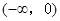 ,
,
(Ⅲ)当 时,由(Ⅱ)可知
时,由(Ⅱ)可知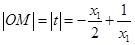 .
.
类似可得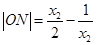 .
.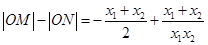 .
.
由①可知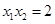 .
.
从而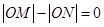 .
.
当 时,有相同的结果
时,有相同的结果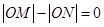 .
.
所以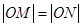 .
.
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
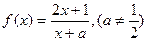 ,
, ,证明
,证明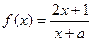 在区间
在区间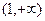 上是增函数;
上是增函数;
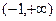 上是单调函数,试求实数
上是单调函数,试求实数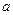 的取值范围。
的取值范围。
 上的函数
上的函数 的图象如右图所示
的图象如右图所示
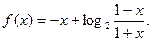
 的值;
的值; 在定义域内的单调性并给予证明.
在定义域内的单调性并给予证明. (
( )的图象与反比例函数
)的图象与反比例函数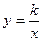 图象相交于点
图象相交于点 ,已知点
,已知点 的坐标为
的坐标为 ,点
,点 在第三象限内,且
在第三象限内,且 的面积为
的面积为 (
( 为坐标原点)
为坐标原点)
 的值;
的值; 轴的另一个交点为
轴的另一个交点为 ,
, 点为线段
点为线段
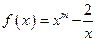 ,且
,且 。
。 的值;
的值; 的奇偶性;
的奇偶性; 上的单调性,并给予证明。
上的单调性,并给予证明。